7.33: Two Photon Interference - Matrix Mechanics Approach
- Page ID
- 142561
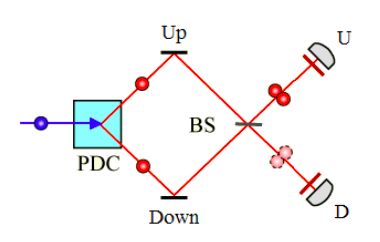
In this experiment a down converter, DC, transforms an incident photon into two lower energy photons. One photon takes the upper path and the other the lower path or vice versa. The results of this experiment are that both photons are detected at either U or D. One photon is never detected at U while the other is detected at D. A quantum mechanical analysis of this phenomena is provided below.
Orthonormal basis states:
Photon moving in up-direction:
\[ u = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
\[ u^T u = 1 \nonumber \]
Photon moving in down-direction:
\[ d = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
\[ d^T d = 1 \nonumber \]
\[ u^T d = 0 \nonumber \]
Operators:
Operator for interaction with the mirror:
\[ M = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \nonumber \]
Operator for interaction with a 50/50 beam splitter:
\[ BS = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \nonumber \]
A 90o phase shift between transmission and reflection at the beam splitter is required to satisfy energy conservation. By convention the phase shift is assigned to reflection.
The down-converter creates the following entangled state:
\[ |Psi_b \rangle = \frac{ \left[|u \rangle_1 |d \rangle_2 + d \rangle_1 u \rangle_2 \right]}{2 ^ \frac{1}{2}} \nonumber \]
This is a symmetric state because photons are bosons.
After creation in the down-converter, both photons interact with a mirror and a beam splitter before reaching a detector, either U or D. To be detected at the U-detector the photon must be moving in the up-direction (photon state = |u>). To be detected at the D-detector the photon must be moving in the down-direction (photon state = |d>). The probabilities for the four possible experimental outcomes are calculated below.
Both photons arrive at the U-detector: \( |_1 \langle u |_2 \langle u | \textbf{BS ~ M} | \Psi_b \rangle |^2\).
\[ \left[ \left| \frac{(u^T BS M u) (u^T BS M d) + (u^T BS M d) (u^T BS M u)}{ \sqrt{2}} \right| \right]^2 = 0.5 \nonumber \]
Both photons arrive at the D-detector: \( |_1 \langle d |_2 \langle d | \textbf{BS ~ M} | \Psi_b \rangle |^2\).
\[ \left[ \left| \frac{(d^T BS M u) (d^T BS M d) + (d^T BS M d) (d^T BS M u)}{ \sqrt{2}} \right| \right]^2 = 0.5 \nonumber \]
Photon 1 arrives at the U-detector and photon 2 arrives at the D-detector: \( |_1 \langle u |_2 \langle d | \textbf{BS ~ M} | \Psi_b \rangle |^2\).
\[ \left[ \left| \frac{(u^T BS M u) (d^T BS M d) + (u^T BS M d) (d^T BS M u)}{ \sqrt{2}} \right| \right]^2 = 0 \nonumber \]
Photon 1 arrives at the D-detector and photon 2 arrives at the U-detector: \( |_1 \langle d |_2 \langle u | \textbf{BS ~ M} | \Psi_b \rangle |^2\).
\[ \left[ \left| \frac{(d^T BS M u) (u^T BS M d) + (d^T BS M d) (u^T BS M u)}{ \sqrt{2}} \right| \right]^2 = 0 \nonumber \]
If the experiment could be performed with fermions, they would be created in the following anti-symmetric entangled state:
\[ |Psi_f \rangle = \frac{ \left[|u \rangle_1 |d \rangle_2 - d \rangle_1 u \rangle_2 \right]}{2 ^ \frac{1}{2}} \nonumber \]
As the analysis below shows, the results for fermions would be exactly opposite to those for bosons. Two fermions would never arrive at the same detector.
Both fermions arrive at the U-detector: \( |_1 \langle u |_2 \langle u | \textbf{BS ~ M} | \Psi_f \rangle |^2\)
\[ \left[ \left| \frac{(u^T BS M u) (u^T BS M d) - (u^T BS M d) (u^T BS M u)}{ \sqrt{2}} \right| \right]^2 = 0 \nonumber \]
Both fermions arrive at the D-detector: \( |_1 \langle d |_2 \langle d | \textbf{BS ~ M} | \Psi_f \rangle |^2\)
\[ \left[ \left| \frac{(d^T BS M u) (d^T BS M d) - (d^T BS M d) (d^T BS M u)}{ \sqrt{2}} \right| \right]^2 = 0 \nonumber \]
Fermion 1 arrives at the U-detector and fermion 2 arrives at the D-detector: \( |_1 \langle u |_2 \langle d | \textbf{BS ~ M} | \Psi_f \rangle |^2\)
\[ \left[ \left| \frac{(u^T BS M u) (d^T BS M d) - (u^T BS M d) (d^T BS M u)}{ \sqrt{2}} \right| \right]^2 = 0.5 \nonumber \]
Fermion 1 arrives at the D-detector and fermion 2 arrives at the U-detector: \( |_1 \langle d |_2 \langle u | \textbf{BS ~ M} | \Psi_f \rangle |^2\)
\[ \left[ \left| \frac{(d^T BS M u) (u^T BS M d) - (d^T BS M d) (u^T BS M u)}{ \sqrt{2}} \right| \right]^2 = 0.5 \nonumber \]
The results of this tutorial enable us to formulate a sociology for bosons and fermions: bosons are gregarious and enjoy companionship; fermions are anti-social and prefer solitude.
But why do bosons always end up at the same detector and fermions (hypothetically) always end up at different detectors? Why in both cases do half of the possible outcomes not occur? Are the bosons and fermions interfering with each other directly? Is there a subtle attractive interaction between bosons and an equally subtle, non-electrostatic, repulsive interaction between fermions?
Not according to Roy Glauber who said, "The things that interfere in quantum mechanics are not particles. They are probability amplitudes for certain events. It is the fact that probability amplitudes add up like complex numbers that accounts for all quantum mechanical interferences." [American Journal of Physics 63, 12 (1995)]
The analysis used in this tutorial clearly illustrates Glauber's assertion.
Reference: Greenberger, D.M.; Horne, M.A.; Zeilinger, A. Physics Today, 1993, 44(8), 22.

