7.24: Optical Activity - A Quantum Perspective

Optical activity is the rotation of linearly polarized light as it advances through a chiral medium. The quantum explanation for optical rotation is based on the fact that linearly polarized light can be written as a superposition of left and right circularly polarized light, which possess angular momentum (see Appendix).

\[ L = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} \nonumber \]

\[ R = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} \nonumber \]

This is demonstrated for vertical, horizontal and Θ polarized light.

\[ V = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]

\[ \frac{1}{ \sqrt{2}} (R + L) \rightarrow \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]

\[ H = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]

\[ \frac{i}{ \sqrt{2}} (L-R) \rightarrow \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]

\[ \Theta = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \nonumber \]

\[ \frac{1}{ \sqrt{2}} (e^{-i \theta} R + e^{i \theta} L) ~simplify \rightarrow \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \nonumber \]

To proceed to a quantum interpretation for optical activity, we assume that \( | \theta \rangle\) polarized light entering a chiral medium will be in the state \( | \theta + \alpha x \rangle\) after traveling a distance x, where α is the optical activity. Our immediate goal is to find the quantum operator for such a process. By analogy with the time‐dependent Schrödinger equation, \( i \frac{h}{2 \pi} \frac{d}{dt} \Psi = H \Psi\), R. L. Martin (Basic Quantum Mechanics, page 30) suggests the following differential equation to describe the spatial evolution of polarization in a chiral medium.

\[ i \frac{d}{dx} \Psi ( \theta , \alpha , x) = K \Psi ( \theta , \alpha , x) \nonumber \]

where

\[ \Psi ( \theta , \alpha , x) = \begin{pmatrix} \cos ( \theta + \alpha x) \\ \sin ( \theta + \alpha x) \end{pmatrix} \nonumber \]

Since αx is an angle, id/dx is an angular momentum operator and what follows determines its matrix representation. Consulting the Appendix we see that it is α times the photon angular momentum operator.

Substitution of ψ yields,

\[ i \alpha \begin{pmatrix} - \sin ( \theta + \alpha x) \\ \cos ( \theta + \alpha x) \end{pmatrix} = K \begin{pmatrix} \cos ( \theta + \alpha x) \\ \sin ( \theta + \alpha x) \end{pmatrix} \nonumber \]

which requires

\[ K = \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} \nonumber \]

\[ i \frac{d}{dx} \begin{pmatrix} \cos ( \theta + \alpha x) \\ \sin ( \theta + \alpha x) \end{pmatrix} \rightarrow \begin{pmatrix} - \alpha \sin ( \theta + \alpha x) \\ \alpha \cos ( \theta + \alpha x) \end{pmatrix} \nonumber \]

\[ \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} \begin{pmatrix} \cos ( \theta + \alpha x) \\ \sin ( \theta + \alpha x) \end{pmatrix} \rightarrow \begin{pmatrix} - \alpha \sin ( \theta + \alpha x) \\ \alpha \cos ( \theta + \alpha x) \end{pmatrix} \nonumber \]

Because they play an essential role in understanding optical rotation, we pause briefly to show that |R > and |L > are eigenvectors of K with eigenvalues α and ‐α respectively.

\[ \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} R \rightarrow \begin{pmatrix} \frac{ \sqrt{2} \alpha}{2} \\ \frac{ \sqrt{2} \alpha i}{2} \end{pmatrix} \nonumber \]

\[ \alpha \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} \nonumber \]

\[ \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} L \rightarrow \begin{pmatrix} - \frac{ \sqrt{2} \alpha}{2} \\ \frac{ \sqrt{2} \alpha i}{2} \end{pmatrix} \nonumber \]

\[ - \alpha \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} \nonumber \]

Integration of the differential equation describing the change in polarization during propagation through an optically active medium yields the sought after polarization spatial evolution operator.

\[ \Psi_{final} = e^{-iKx} \Psi_{initial} = e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \Psi_{initial} \nonumber \]

where

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} ~simplify~ \rightarrow \begin{pmatrix} \cos ( \alpha x) & - \sin ( \alpha x) \\ \sin ( \alpha x) & \cos ( \alpha x) \end{pmatrix} \nonumber \]

This demonstrates that the spatial evolution operator is a matrix which rotates the plane of polarization by an angle αx. Now the effect of the operator on vertical, horizontal and Θ polarized light is demonstrated.

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \begin{pmatrix} 1 \\ 0 \end{pmatrix} ~simplify~ \rightarrow \begin{pmatrix} \cos ( \alpha x) \\ \sin ( \alpha x) \end{pmatrix} \nonumber \]

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \begin{pmatrix} 0 \\ 1 \end{pmatrix} ~simplify~ \rightarrow \begin{pmatrix} - \sin ( \alpha x) \\ \cos ( \alpha x) \end{pmatrix} \nonumber \]

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} ~simplify~ \rightarrow \begin{pmatrix} \cos ( \theta + \alpha x) \\ \sin ( \theta + \alpha x) \end{pmatrix} \nonumber \]

Next the circular polarization states are operated on.

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} ~simplify~ \rightarrow \begin{pmatrix} \frac{ \sqrt{2} e^{ - \alpha x i}}{2} \\ \frac{ \sqrt{2} e^{ - \alpha x i} i}{2} \end{pmatrix} \nonumber \]

or

\[ e^{-i \alpha x} \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} \nonumber \]

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} ~simplify~ \rightarrow \begin{pmatrix} \frac{ \sqrt{2} e^{ \alpha x i}}{2} \\ - \frac{ \sqrt{2} e^{ - \alpha x i} i}{2} \end{pmatrix} \nonumber \]

or

\[ e^{i \alpha x} \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} \nonumber \]

We see that propagation through the chiral medium causes a phase shift in the circular polarization states. This turns out to be of essential importance in understanding the rotation of plane polarized light which occurs during propagation. It was shown previously, that plane polarized light can be expressed as a superposition of left and right circularly polarized light. Letʹs rewrite that superposition using the phase relation just demonstrated. For the sake of computational simplicity we will use α = 1, and because the phase factor is a trigonometric function we will express distance in units of π.

Our example involves a vertically polarized light source illuminating a chiral medium. At the point of entry, x = 0, we show that the light is indeed vertically polarized.

\( x = 0\):

\[ \frac{1}{2} \left[ exp (-i \alpha x) \begin{pmatrix} 1 \\ i \end{pmatrix} + exp(i \alpha x) \begin{pmatrix} 1 \\ -i \end{pmatrix} \right] = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]

This formulation shows that as light penetrates the chiral medium, the vertically polarized photon is rotated.

\( x = \frac{ \pi}{4}\):

\[ \frac{1}{2} \left[ exp (-i \alpha x) \begin{pmatrix} 1 \\ i \end{pmatrix} + exp(i \alpha x) \begin{pmatrix} 1 \\ -i \end{pmatrix} \right] = \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} \nonumber \]

\( x = \frac{ \pi}{2}\):

\[ \frac{1}{2} \left[ exp (-i \alpha x) \begin{pmatrix} 1 \\ i \end{pmatrix} + exp(i \alpha x) \begin{pmatrix} 1 \\ -i \end{pmatrix} \right] = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]

Of course, the same results are obtained by operating directly on |v >.

\( x = 0\):

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \begin{pmatrix} 1 \\ 0 \end{pmatrix} ~simplify~ \rightarrow \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]

\( x = \frac{ \pi}{4}\):

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \begin{pmatrix} 1 \\ 0 \end{pmatrix} ~simplify~ \rightarrow \begin{pmatrix} \frac{ \sqrt{2}}{2} \\ \frac{ \sqrt{2}}{2} \end{pmatrix} = \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} \nonumber \]

\( x = \frac{ \pi}{2}\):

\[e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \begin{pmatrix} 1 \\ 0 \end{pmatrix} ~simplify~ \rightarrow = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]

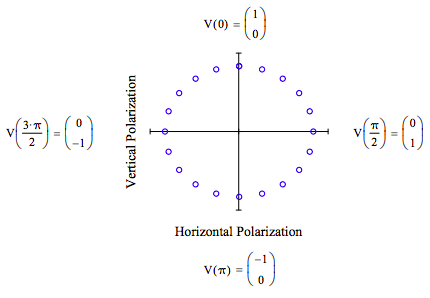
The juxtaposition of the two sets of calculations suggests that the rotation of plane polarized light in a chiral medium is due to phase changes in its left, |L >, and right, |R >, circularly polarized components during propagation. Couching the explanation in terms of |L > and |R > is further justified by the fact that they are the eigenstates of the Hermitian K matrix which produces the rotation. A picture of the progression of the angle of rotation as light advances through a chiral medium can be created by plotting the vertical vs horizontal components of the polarization vector as a function of x.

\( x = 0, .1 \pi .. 2 \pi\):

\[ V(x) = e^{-i \begin{pmatrix} 0 & -i \alpha \\ i \alpha & 0 \end{pmatrix} x} \begin{pmatrix} 1 \\ 0 \end{pmatrix} ~simplify~ \rightarrow \begin{pmatrix} \cos x \\ \sin x \end{pmatrix} \nonumber \]

for α = 1.

Appendix

The angular momentum operator for photons in atomic units is \( M = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}\), which means, of course, that K = αM. |R > and |L > are eigenvectors of M with eigenvalues +1 and ‐1, respectively. As shown earlier they are eigenvectors of K with eigenvalues α and ‐α, respectively.

\[ M R = \begin{pmatrix} 0.707 \\ 0.707i \end{pmatrix} \nonumber \]

\[ \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} \nonumber \]

\[ M L = \begin{pmatrix} -0.707 \\ 0.707i \end{pmatrix} \nonumber \]

\[ -\frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} \nonumber \]

The linearly polarized states are not eigenvectors of M and have angular momentum expectation values of zero.

\[ \begin{pmatrix} 1 & 0 \end{pmatrix} M \begin{pmatrix} 1 \\ 0 \end{pmatrix} = 0 \nonumber \]

\[ \begin{pmatrix} 0 & 1 \end{pmatrix} M \begin{pmatrix} 0 \\ 1 \end{pmatrix} = 0 \nonumber \]

\[ \begin{pmatrix} \cos \theta & \sin \theta \end{pmatrix} M \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \rightarrow 0 \nonumber \]