7.20: Quantum Seeing in the Dark - A Matrix-Tensor Analysis
- Page ID
- 141610
The following device consisting of an equal-arm polarization interferometer, a switchable mirror and a polarization rotator appears in "Quantum Seeing in the Dark" by Kwiat, Weinfurter and Zeilinger in the November 1996 issue of Scientific American. It is used to illustrate the concept of interaction-free measurement. In what follows I analyze its operation using matrix and tensor algebra.
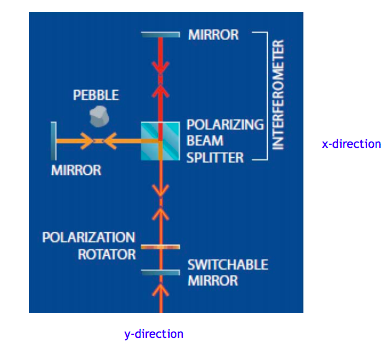
The polarizing beam splitter transmits horizontally polarized photons and reflects those that are vertically polarized. Therefore, vector states which contain direction of motion and polarization information of the photons are required. This is accomplished using vector tensor multiplication.
Vertical motion:
\[ x = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
Horizontal motion:
\[ x = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
Horizontal polarization:
\[ x = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
Vertical polarization:
\[ x = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
Photon direction of propagation and polarization states:
\[ xh = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
\[ xh = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ xv = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
\[ xv = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ yh = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
\[ yh = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \nonumber \]
\[ yv = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
\[ yv = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \nonumber \]
Now the matrix which represents a polarizing beam splitter which transmits horizontally polarized photons and reflects vertically polarized photons is constructed.
\[ PBS = (xh) xh^T + (yv)xv^T + (yh)yh^T + (xv)yv^T \nonumber \]
\[ PBS = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix} \nonumber \]
The matrix representing the polarization rotator is:
\[ Rot( \theta) = \begin{pmatrix} \cos \theta & - \sin \theta & 0 & 0 \\ \sin \theta & \cos \theta & 0 & 0 \\ 0 & 0 & \cos \theta & -\sin \theta \\ 0 & 0 & \sin \theta & \cos \theta \end{pmatrix} \nonumber \]
It is unnecessary to include matrices representing the mirrors because they simply reflect the photon back to the beam splitter for a second encounter. First consider the case in which there is no obstructing pebble in the y-branch of the interferometer. A horizontally polarized photon enters the system and the polarization rotator rotates the polarization by 15 degrees (π/12) toward the vertical. This results in a superposition of |xh> and |xv>. This photon state enters the interferometer, |xh> and |xv> are temporarily split, and then recombined to reform the entering superposition. After one cycle the photon's polarization state is as follows.
\[ \left( PBS (PBS) Rot \left( \frac{ \pi}{12} \right) \right)^1 xh = \begin{pmatrix} 0.966 \\ 0.259 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ 0.966xh + 0.259xv = \begin{pmatrix} 0.966 \\ 0.259 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
The bottom mirror reflects the photon back to the polarization rotator for another pass through the interferometer. After six cycles the switchable mirror at the bottom of the device releases a vertically polarized photon. In other words, if the equal arm interferometer does not have an obstruction in the y-branch, the initial horizontally polarized photon is rotated stepwise to the vertical polarization state.
\[ \left( PBS (PBS) Rot \left( \frac{ \pi}{12} \right) \right)^6 xh = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ \left[ \left| xv^T \left( PBS (PBS) Rot \left( \frac{ \pi}{12} \right) \right)^6 xh \right| \right]^2 = 1 \nonumber \]
Practically this would be confirmed by having a polarizing beam splitter (PBS) at the output channel of the device. As shown below the photon will be detected at the vertical (y-direction) port and not the horizontal (x-direction) port.
\[ \left[ \left| yv^T PBS \left( PBS (PBS) Rot \left( \frac{ \pi}{12} \right) \right)^6 xh \right| \right]^2 = 1 \nonumber \]
\[ \left[ \left| xh^T PBS \left( PBS (PBS) Rot \left( \frac{ \pi}{12} \right) \right)^6 xh \right| \right]^2 = 0 \nonumber \]
The presence of the pebble takes the y-branch of the interferometer "out of play." Under these circumstances the polarizing beam splitter is represented by the following matrix.
\[ PBS' = (xh) xh^T \nonumber \]
\[ PBS' = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} \nonumber \]
Now after six cycles there is a 66% probability that the mirror will release a horizontally polarized photon. The other 34% of the time the photon will be absorbed by the pebble.
\[ \left( PBS' (PBS') Rot \left( \frac{ \pi}{12} \right) \right)^6 xh = \begin{pmatrix} 0.812 \\ 0 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ \left[ \left| xh^T \left( PBS' (PBS') Rot \left( \frac{ \pi}{12} \right) \right)^6 xh \right| \right]^2 = 0.66 \nonumber \]
As noted earlier, the actual device would have a final PBS after the switchable mirror, showing that a vertical photon is never detected (it has been absorbed) and a horizontal photon is recorded with a 0.66 probability.
\[ \left[ \left| yv^T PBS \left( PBS' (PBS') Rot \left( \frac{ \pi}{12} \right) \right)^6 xh \right| \right]^2 = 0 \nonumber \]
\[ \left[ \left| xh^T PBS \left( PBS' (PBS') Rot \left( \frac{ \pi}{12} \right) \right)^6 xh \right| \right]^2 = 0.66 \nonumber \]
Recall that in the absence of the obstruction the mirror releases a vertically polarized photon 100% of the time. The detection of a horizontally polarized photon indicates the presence of the pebble without an interaction with the pebble. With six cycles interaction-free measurement occurs about two thirds of the time. Increasing the number of cycles increases the utility of the device. For thirty cycles (a π/60 polarization rotation per cycle) a horizontally polarized photon is detected 92% of the time: interaction-free measurement occurs 92% of the time.
\[ \left[ \left| xh^T \left( PBS' (PBS') Rot \left( \frac{ \pi}{60} \right) \right)^{30} xh \right| \right]^2 = 0.92 \nonumber \]
\[ \left[ \left| xh^T PBS \left( PBS' (PBS') Rot \left( \frac{ \pi}{60} \right) \right)^{30} xh \right| \right]^2 = 0.92 \nonumber \]
Increasing the number of cycles increases the reliability of the method, but is also experimentally very challenging.

