7.17: Polarized Light and Quantum Mechanics
- Page ID
- 141607
The Linear Superposition
Unpolarized light consists of photons of all possible polarization angles. A photon polarized at an angle \( \theta\) with respect to the vertical can be written as a linear superposition of a vertically polarized photon, \( | v \rangle\), and a horizontally polarized photon, \( | h \rangle\). \( | v \rangle\) and \( | h \rangle\) are the polarization basis states.
\[ | \theta \rangle = | v \rangle \langle v | \theta \rangle + | h \rangle \langle h | \theta \rangle \nonumber \]
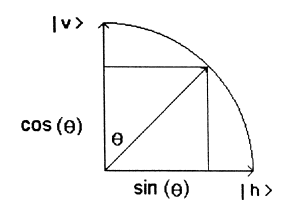
From the figure above it can be seen that the projection of \( | \theta \rangle\) onto \( | v \rangle\) and \( | h \rangle\) are \( \cos \theta\) and \( \sin \theta\) respectively.
\[ | \theta \rangle = | v \rangle \cos \theta + | h \rangle \sin \theta \nonumber \]
The probability that a photon polarized at an angle \( \theta\) will pass a vertical polarizer is
\[ | \langle | \theta \rangle | ^2 = \cos^2 \theta \nonumber \]
By integrating this function over all possible angles we find that half of the incident light passes through a vertical polarizer. See the figure below.
\[ \frac{ \int_{0}^{2 \pi} \cos^2 \theta d \theta}{2 \pi} = 0.5 \nonumber \]
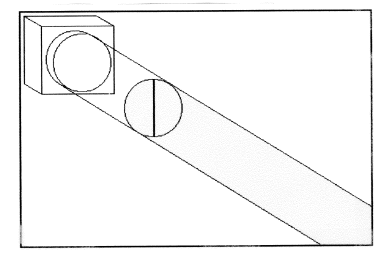
The photons that pass the vertical polarizer are now vertically polarized. That is they are eigenfunctions of that measurement operator.
The probability that a vertically polarized photon will pass a second filter that is vertically polarized is one.
\[ | \langle v | v \rangle |^2 = \cos^2 0^o = 1 \nonumber \]
The probability that a vertically polarized photon will pass a second filter that is horizontally polarized is zero.
\[ | \langle h | v \rangle |^2 = \cos^2 90^o = 0 \nonumber \]
The vertically polarized photon can be written as linear superposition of any other set of orthogonal basis states, for example \( |45^o \rangle\) and \( | -45^o \rangle\).
\[ |v \rangle = |45^o \rangle \langle 45^o | v \rangle + | -45^o \rangle \langle -45^o | v \rangle \nonumber \]
\[ |v \rangle = |45^o \rangle \cos 45^o + | -45^o \rangle \cos -45^o \nonumber \]
\[ |v \rangle = |45^o \rangle 0.707 + | -45^o \rangle 0.707 \nonumber \]
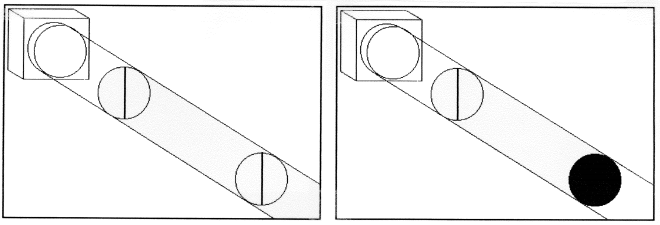
Now if a 45o polarizer is inserted in between the vertical and horizontal polarizers photons get through the horizontal polarizer that stopped them previously (see the last figure).
Here's the explanation. The probability that a vertically polarized photon will get through a polarizer oriented at an angle of 45o is 0.5. See the figure below.
\[ | \langle 45^o | v \rangle |^2 = \cos^2 45^o = 0.5 \nonumber \]
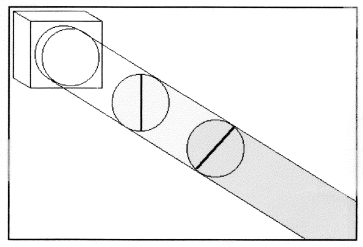
Now the photon is in the state of \( |45^o \rangle\) which can be written as a linear superposition of \( |v \rangle\) and \( \h \rangle\).
\[ |45^o \rangle = |v \rangle \langle v | 45^o \rangle + | h \rangle \langle h | 45^o \rangle \nonumber \]
\[ |45^o \rangle = |v \rangle \cos 45^o + | h \rangle \sin 45^o \nonumber \]
\[ |45^o \rangle = |v \rangle 0.707 + | h \rangle 0.707 \nonumber \]
Thus, the probability that this photon will pass the final horizontally oriented polarizer is
\[ | \langle H | 45^o \rangle |^2 = \sin^2 45^o = 0.5 \nonumber \]
See the figure below.
In this last figure the intensity of the light emerging from the final horizontal polarizing filter can be calculated compactly as
\[ \frac{ \int_{0}^{2 \pi} | \langle h | 45^o \rangle \langle 45^o | v \rangle \langle v | \theta \rangle|^2 d \theta}{2 \pi} = \frac{1}{8} \nonumber \]
The term inside the integral is the probability that a photon with polarization θ will pass through the three filters. This expression is integrated over all values of θ.

