7.12: Polarized Light and Quantum Mechanics

Readily available and inexpensive polarizing films can be used to illustrate many fundamental quantum mechanical concepts. The purpose of this tutorial is to use polarized light to illustrate one of quantum theory’s deepest and most challenging concepts - the linear superposition. According to Richard Feynman the superposition principle “has in it the heart of quantum mechanics” and is its “only mystery.” (1)

Three Polarizer “Paradox”

If two polarizing films are aligned in the same direction light from the first polarizer passes through the second. If the polarizers are opposed at a 90° angle, the polarized light from the first polarizer is stopped by the second. If a third polarizer is sandwiched between the two opposed polarizers at a 45° angle some light gets through the last polarizer.(2, 3) The analysis that follows is based on the quantum mechanical superposition principle. A graphical representation is shown below.

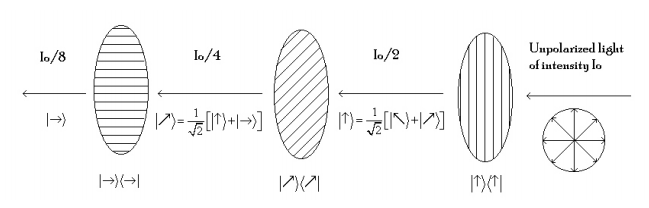
Quantum Mechanical Analysis

A photon polarized at an angle 2 with respect to the vertical can be written as a linear combination (superposition) of a vertically polarized photon, \( |v \rangle\), and a horizontally polarized photon, \( |h \rangle\). We say \( |v \rangle\) and \( |h \rangle\) are the polarization basis states, which means \( \langle v | v \rangle = \langle h|h \rangle = 1\) and \( \langle v | h \rangle = \langle h|v \rangle = 0\).

\[ | \Theta \rangle = | v \rangle \langle v | \Theta \rangle + | h \rangle \langle h | \Theta \rangle \nonumber \]

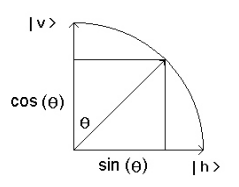
From this figure we see that the projections of \( | \Theta \rangle\), onto \( |v \rangle \langle \langle v | \Theta \rangle \rangle\) and \( |h \rangle \langle \langle h | \Theta \rangle \rangle\) are \( \cos \Theta\) and \( \sin \Theta\), respectively.

\[ |\Theta \rangle = | v \rangle \cos \Theta + |h \rangle \sin \Theta \nonumber \]

The probability that a photon polarized at an angle \(\Theta\) will pass a vertical polarizer is

\[ | \langle v | \Theta \rangle |^2 = \cos^2 \Theta \nonumber \]

The light incident on the first polarizer is unpolarized, but the photons that pass the vertical polarizer are vertically polarized. In other words the photons are eigenfunctions of the measurement operator, which in this case is a vertically oriented linear polarizer. At this point only two experiments have definite outcomes.

1. The probability that vertically polarized photons will pass a second filter that is also vertically polarized is one. It is certain that a vertically polarized photon will pass a vertically polarized filter. \[ | \langle v | v \rangle | ^2 = \cos^2 0 = 1 \nonumber \]
2. The probability that vertically polarized photons will pass a second filter that is horizontally polarized is zero. It is certain that a vertically polarized photon will not pass a horizontally polarized filter.

\[ | \langle h | v \rangle |^2 = \cos^2 90 = 0 \nonumber \]

For any other orientation of the second filter, quantum mechanics can only predict the probability that a vertically polarized photon will pass, and that probability is, of course,

\[ | \langle \Theta | v \rangle |^2 = \cos^2 \Theta \nonumber \]

Now a vertically polarized photon may be written as a linear superposition of any other orthogonal basis states, for example \( |45^o \rangle\), and \( |-45^o \rangle\).

\[ \begin{align} |v \rangle &= | 45^o \rangle \langle 45^o | v \rangle +|- 45^o \rangle \langle -45^o | v \rangle \\[4pt] &= | 45^o \rangle \cos 45^o +|- 45^o \rangle \cos 45^o \\[4pt] &= | 45^o \rangle 0.707 +|- 45^o \rangle 0.707 \end{align} \nonumber \]

If a 45° polarizer is inserted between the vertical and horizontal polarizers photons get through the horizontal polarizer that stopped them previously. Here is the quantum mechanical explanation. The probability that a vertically polarized photon will get through a polarizer oriented at an angle of 45° is, by eqns (7), 1/2.

\[ | \langle 45^o | v \rangle |^2 = \cos^2 45^o = \frac{1}{2} \nonumber \]

At this point the photon is in the state \( |45^o \rangle\), and according to the superposition principle a photon in this state can be written as a linear combination of \( |v \rangle\) and \( |h \rangle\).

\[ |45^o \rangle = | v \rangle \langle v|45^o \rangle + |h \rangle \langle h + 45^o \rangle \nonumber \]

\[ |45^o \rangle = | v \rangle \cos45^o + |h \rangle \sin 45^o \nonumber \]

Therefore, the probability that this photon will pass the final horizontally oriented polarizer is

\[ | \langle h | 45^o \rangle |^2 = \sin^2 45^o = \frac{1}{2} \nonumber \]

Alternatively, the probability that a photon emerging from the vertical polarizer will pass through the final horizontal polarizer in the presence of an intermediate 45° polarizer can be calculated as follows:

\[ | \langle h | 45^o \rangle \langle 45^o | v \rangle |^2 = | \sin^2 45^o \cos^2 45^o |^2 = \frac{1}{4} \nonumber \]

In other words, half of the photons that emerge from the vertical polarizer pass the 45° polarizer, and half of those pass the final horizontal polarizer. So 25% of the photons that pass the initial vertical polarizer also pass the final horizontal polarizer.

Unpolarized Light

The unpolarized light illuminating the first polarizer is a 50-50 mixture of any orthogonal set of polarizer angles – (0°, 90°), (-45°, 45°), or in the general case (\( \left(\Theta, \Theta + \frac{ \pi}{2} \right)\).(4) A mixture cannot be represented by a single wave function, so the expectation value for a mixture of unpolarized photons to pass a vertical polarizer is calculated as follows:

\[ \langle V \rangle = \sum_i p_i \langle \Psi_i | \hat{V} | \Psi_i \rangle \nonumber \]

where V represents the operator associated with the vertical polarizer, and p_i is the fraction of photons in the state \( | \Psi_i \rangle\).

For the general case of a beam of unpolarized light incident on a vertical polarizer the expectation value for transmission is,

\[ \langle V \rangle = \frac{1}{2} \left\langle \Theta \right| \hat{V} \left| \Theta \right\rangle + \frac{1}{2} \left\langle \Theta + \frac{ \pi}{2} \right| \hat{V} \left| \Theta + \frac{ \pi}{2} \right\rangle \label{267.16} \]

Since \( \hat{V} = | v \rangle \langle v |\), Equation \ref{267.16} can be written as,

\[ \langle V \rangle = \frac{1}{2} \left\langle \Theta | v \right\rangle \left\langle v | \Theta \right\rangle + \frac{1}{2} \left\langle \Theta + \frac{ \pi}{2} | v \right\rangle \left\langle v | \Theta + \frac{ \pi}{2} \right\rangle \nonumber \]

This expression simplifies to,

\[ \langle V \rangle = \frac{1}{2} \left[ \cos^2 \Theta + \cos^2 \left( \Theta + \frac{ \pi}{2} \right) \right] = \frac{1}{2} \nonumber \]

References

1. Feynman, R. P.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics, Vol. 3; Addison-Wesley: Reading, 1965
2. N. David Mermin, "Spooky Action at a Distance: Mysteries of the Quantum Theory," in The Great Ideas Today 1988, Encyclopedia Britannica, Inc., Chicago, pp 2-53.
3. Nick Herbert, Quantum Reality: Beyond the New Physics, Anchor Books, New York, 1985, pp 182-185.
4. H. J. Lipkin, Quantum Mechanics, North-Holland, Amsterdam, 1973, pp 12-14.