7.6: The Polarizing Beam Splitter and the Superposition Principle
- Page ID
- 137803
A polarizing beam splitter (PBS) and PBS interferometer (PBSI) can be used to illustrate the superposition principle. In this analysis the quantum math explaining the operation of a PBSI is presented.
A PBS transmits vertically polarized photons, \(|v\rangle\), and reflects horizontally polarized photons, |h>. As the diagrams below show, the photons propagate in the x- or y-directions, \(|x\rangle\) and \(|y\rangle\). The interaction of \(|v\rangle\) and \(|h\rangle\) photons emitted by the source in the x-direction, \(|x\rangle\), with the PBS is summarized in the two equations below. Note that we need to keep track of two degrees of freedom, direction of propagation and polarization state. This information is stored in the product of two Dirac kets, | >| >.
\[ S \rightarrow |x \rangle |v \rangle \xrightarrow{PBS} |x \rangle |v \rangle \nonumber \]
\[ S \rightarrow |x \rangle |h \rangle \xrightarrow{PBS} |y \rangle |h \rangle \nonumber \]
We will proceed with our analysis assuming that the source emits a diagonally polarized photon, |x>|d>. A diagonally polarized photon is an even superposition of being vertically and horizontally polarized. Thus the photon state incident on the PBS is,
\[ S \rightarrow |x \rangle |d \rangle = |x \rangle \bigg[ \frac{1}{ \sqrt{2}} |v \rangle + \frac{1}{ \sqrt{2}} |h \rangle \bigg] = \frac{1}{ \sqrt{2}} |x \rangle |v \rangle + \frac{1}{ \sqrt{2}} |x \rangle |h \rangle \nonumber \]
After the interaction with the PBS and the mirrors the photon state is,
\[ \frac{1}{ \sqrt{2}} |x \rangle |v \rangle + \frac{1}{ \sqrt{2}} |x \rangle |h \rangle \xrightarrow{PBS} \frac{1}{ \sqrt{2}} |x \rangle |v \rangle + \frac{1}{ \sqrt{2}} |y \rangle |h \rangle \xrightarrow{M} \frac{1}{ \sqrt{2}} |y \rangle |v \rangle + \frac{1}{ \sqrt{2}} |x \rangle |h \rangle \nonumber \]
The photon is in an even superposition of moving in the y-direction with vertical polarization and moving in the x-direction with horizontal polarization. For a statistically meaningful number of experiments, this analysis predicts that in 50% of the experiments the photon will appear at Dx with horizontal polarization and in 50% it will appear at Dy with vertical polarization. This is confirmed by experiment.
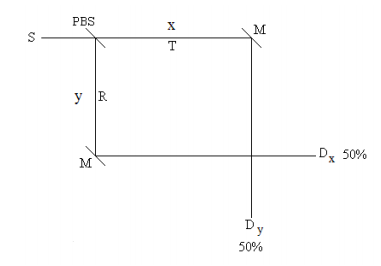
Now, at the photon path intersection just before the detectors a second PBS is inserted as shown below. This second PBS recombines the photon paths and creates a PBSI.
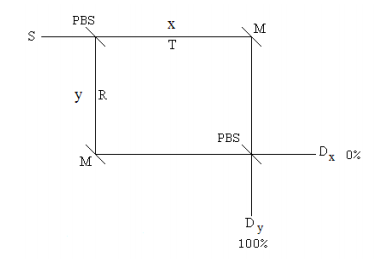
The interaction of the photon with the second PBS yields the following state.
\[ \frac{1}{ \sqrt{2}} |y \rangle |v \rangle + \frac{1}{ \sqrt{2}} |x \rangle |h \rangle \xrightarrow{PBS} \frac{1}{ \sqrt{2}} |y \rangle |v \rangle + \frac{1}{ \sqrt{2}} |y \rangle |h \rangle = | y \rangle \bigg[ \frac{1}{ \sqrt{2}} |v \rangle + \frac{1}{ \sqrt{2}} |h \rangle \bigg] = |y \rangle |d \rangle \nonumber \]
The photon is always detected at Dy with diagonal polarization.
In summary, the source emits a photon in the x-direction in a v-h superposition state. Inside the interferometer the photon is in a superposition of both direction of propagation and polarization state. It emerges from the interferometer in the original polarization state |d>, but moving in the y-direction.
\[ |x \rangle | d \rangle = |x \rangle \bigg[ \frac{1}{ \sqrt{2}} |v \rangle + \frac{1}{ \sqrt{2}} |h \rangle \bigg] = \frac{1}{ \sqrt{2}} |x \rangle |v \rangle + \frac{1}{ \sqrt{2}} |x \rangle |h \rangle \nonumber \]
PBS
\[ \frac{1}{ \sqrt{2}} |x \rangle |v \rangle + \frac{1}{ \sqrt{2}} |y \rangle |h \rangle \nonumber \]
M
\[ \frac{1}{ \sqrt{2}} |y \rangle |v \rangle + \frac{1}{ \sqrt{2}} |x \rangle |h \rangle \nonumber \]
PBS
\[ \frac{1}{ \sqrt{2}} |y \rangle |v \rangle + \frac{1}{ \sqrt{2}} |y \rangle |h \rangle = |y \rangle \bigg[ \frac{1}{ \sqrt{2}} |v \rangle + \frac{1}{ \sqrt{2}} |h \rangle \bigg] = |y \rangle |d \rangle \nonumber \]
For an arbitrary polarization state |θ> we have,
\[ |x \rangle | \theta \rangle = |x \rangle \big[ \cos \theta |v \rangle + \sin \theta |h \rangle \big] = |x \rangle \cos \theta | v \rangle + |x \rangle \sin \theta |h \rangle \nonumber \]
PBS
\[ |x \rangle \cos \theta | v \rangle + |y \rangle \sin \theta |h \rangle \nonumber \]
M
\[ |x \rangle \cos \theta | v \rangle + |x \rangle \sin \theta |h \rangle \nonumber \]
PBS
\[ |y \rangle \cos \theta |v \rangle + |y \rangle \sin \theta |h \rangle = |y \rangle \big[ \cos \theta |v \rangle + \sin \theta |h \rangle \big] = |y \rangle \theta \rangle \nonumber \]

