1.46: Which Path Information and the Quantum Eraser (Brief)
- Page ID
- 149261
This tutorial examines the real reason which‐path information destroys the double‐slit diffraction pattern and how the so‐called ʺquantum eraserʺ restores it. The wave function for a photon illuminating the slit screen is written as a superposition of the photon being present at both slits simultaneously. The double‐slit diffraction pattern is calculated by projecting this superposition into momentum space. This is a Fourier transform for which the mathematical details can be found in the Appendix.
\[
| \Psi \rangle=\frac{1}{\sqrt{2}}\left[ | x_{1}\right\rangle+| x_{2} \rangle ] \qquad \Psi(p)=\langle p | \Psi\rangle=\frac{1}{\sqrt{2}}\left[\left\langle p | x_{1}\right\rangle+\left\langle p | x_{2}\right\rangle\right]
\nonumber \]

Attaching polarizers to the slits creates an entangled superposition of the photon being at slit 1 with vertical polarization and at slit 2 with horizontal polarization. This leads to the following momentum distribution at the detection screen. The interference fringes have disappeared leaving a single‐slit diffraction pattern.
\[
| \Psi^{\prime} \rangle=\frac{1}{\sqrt{2}}\left[ | x_{1}\right\rangle | V \rangle+| x_{2} \rangle | H \rangle ] \qquad \Psi^{\prime}(p)=\left\langle p | \Psi^{\prime}\right\rangle=\frac{1}{\sqrt{2}}\left[\left\langle p | x_{1}\right\rangle | V\right\rangle+\left\langle p | x_{2}\right\rangle | H \rangle ]
\nonumber \]
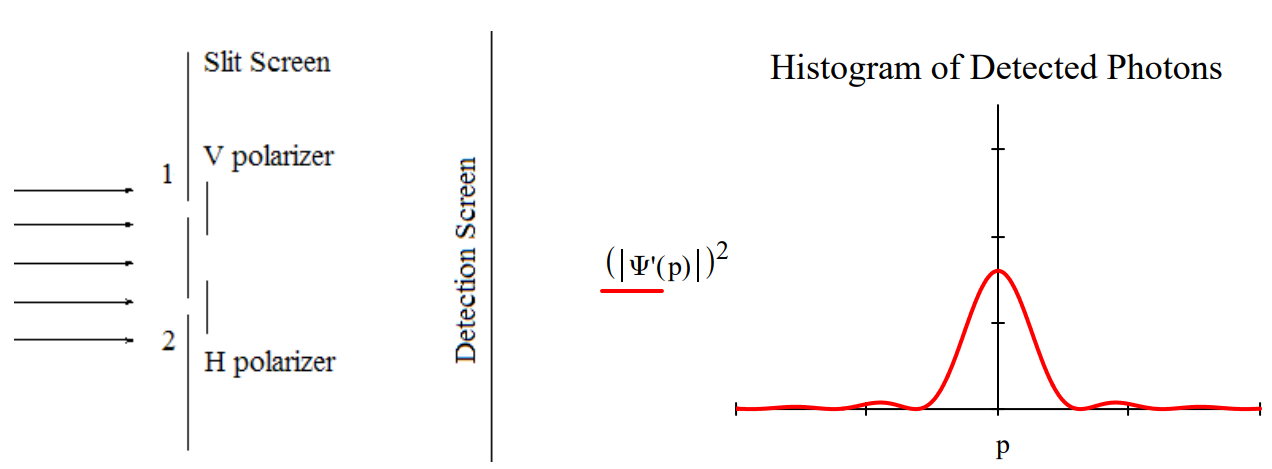
The usual explanation for this effect is that it is now possible to know which slit the photons went through, and that such knowledge destroys the interference fringes because the photons are no longer in a superposition of passing through both slits, but rather a mixture of passing through one slit or the other.
However, a better explanation is that the superposition persists with orthogonal polarization tags, and because of this the interference (cross) terms in the momentum distribution, \(\left|\Psi^{\prime}(p)\right|^{2}\), vanish leaving a pattern at the detection screen which is the sum of two single‐slit diffraction patterns, one from the upper slit and the other from the lower slit.
That this is a reasonable interpretation is confirmed when a so‐called quantum eraser, a polarizer (D) rotated clockwise by 45 degrees relative to the vertical, is placed before the detection screen.
\[
\Psi^{\prime \prime}(p)=\left\langle D | \Psi^{\prime}(p)\right\rangle=\frac{1}{\sqrt{2}}\left[\left\langle p | x_{1}\right\rangle\langle D | V\rangle+\left\langle p | x_{2}\right\rangle\langle D | H\rangle\right]=\frac{1}{2}\left[\left\langle p | x_{1}\right\rangle+\left\langle p | x_{2}\right\rangle\right]
\nonumber \]
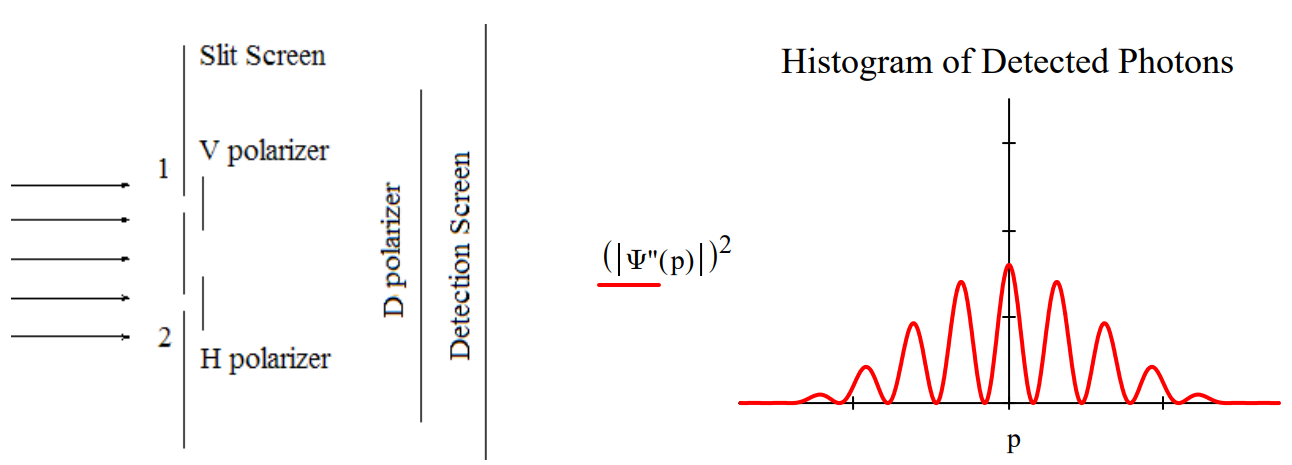
The diagonal polarizer is called a quantum eraser because it appears to restore the interference pattern lost because of the which‐path information provided by the V/H polarizers. However, it is clear from this analysis that the diagonal polarizer doesnʹt actually erase, it simply passes the diagonal component of \(| \Psi^{'} \rangle\) which then shows an attenuated (by half) version of the original interference pattern produced by \(| \Psi \rangle\).
Placing an anti‐diagonal polarizer (rotated counterclockwise by 45 degrees relative to the vertical) before the detection screen causes a 180 degree phase shift in the restored interference pattern.
\[
\Psi^{\prime \prime}(p)=\left\langle A | \Psi^{\prime}(p)\right\rangle=\frac{1}{\sqrt{2}}\left[\left\langle p | x_{1}\right\rangle\langle A | V\rangle+\left\langle p | x_{2}\right\rangle\langle A | H\rangle\right]=\frac{1}{2}\left[\left\langle p | x_{1}\right\rangle-\left\langle p | x_{2}\right\rangle\right]
\nonumber \]
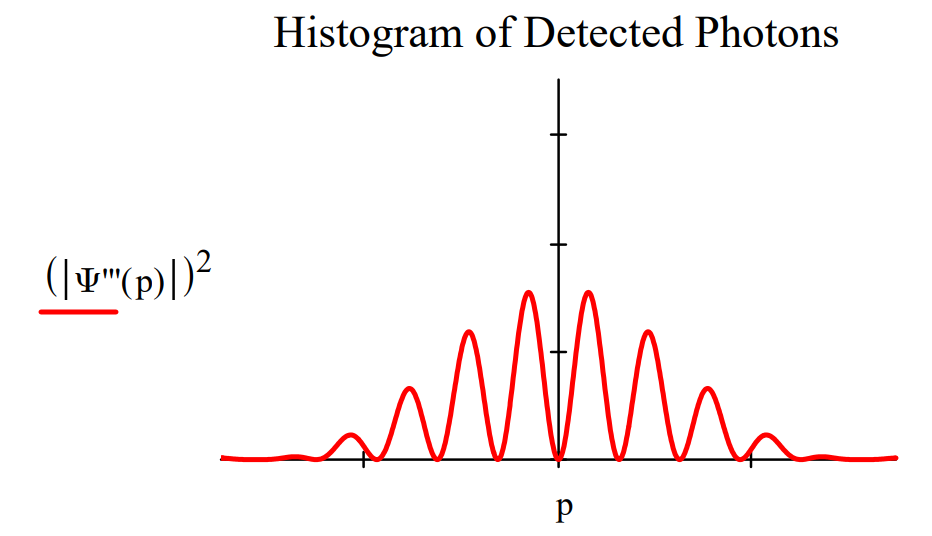
This phase shift is inconsistent with any straightforward explanation based on the concept of erasure of which‐path information. Erasure implies removal of which‐path information. If which‐path information has been removed shouldnʹt the original interference pattern be restored without a phase shift?
Appendix
The V/H polarization which‐path tags and the D/A polarization ʺerasersʺ in vector format:
\[
| \mathrm{V} \rangle=\left( \begin{array}{l}{1} \\ {0}\end{array}\right) | \mathrm{H} \rangle=\left( \begin{array}{l}{0} \\ {1}\end{array}\right) \quad | \mathrm{D} \rangle=\frac{1}{\sqrt{2}} \left( \begin{array}{l}{1} \\ {1}\end{array}\right) \quad | \mathrm{A} \rangle=\frac{1}{\sqrt{2}} \left( \begin{array}{c}{1} \\ {-1}\end{array}\right)\langle\mathrm{D} | \mathrm{V}\rangle=\langle\mathrm{D} | \mathrm{H}\rangle=\langle\mathrm{A} | \mathrm{V}\rangle=\frac{1}{\sqrt{2}}\qquad\langle \mathrm{A} | \mathrm{H}\rangle=-\frac{1}{\sqrt{2}}
\nonumber \]
For infinitesimally thin slits the momentum‐space wave function is,
\[
\Psi(p)=\langle p | \Psi\rangle=\frac{1}{\sqrt{2}}\left[\left\langle p | x_{1}\right\rangle+\left\langle p | x_{2}\right\rangle\right]=\frac{1}{\sqrt{2}}\left[\frac{1}{\sqrt{2 \pi}} \exp \left(-i p x_{1}\right)+\frac{1}{\sqrt{2 \pi}} \exp \left(-i p x_{2}\right)\right]
\nonumber \]
Assuming a slit width \(\delta\) the calculations of \(\Psi\)(p), \(\Psi^{ʹ}\)(p), \(\Psi^{'ʹ}\)(p) and \(\Psi^{''ʹ}\)(p) are carried out as follows:
| Position of first slit: \(\mathrm{x}_{1} \equiv 0\) | Position of second slit: \(\mathrm{x}_{2} \equiv 1\) | Slit width: \(\delta \equiv 0.2\) |
\[
\Psi(\mathrm{p})\equiv\frac{1}{\sqrt{2}}\cdot\left(\int_{\mathrm{x}_{1}-\frac{\delta}{2}}^{\mathrm{x}_{1}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{dx} +\int_{\mathrm{x}_{2}-\frac{\delta}{2}}^{\mathrm{x}_{2}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}\right)
\nonumber \]
For \(\Psi^{ʹ}\)(p) the V/H polarization which‐path tags are added to the two terms of \(\Psi\)(p)
\[
\Psi^{\prime}(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \cdot \left[ \int_{x_{1}-\frac{\delta}{2}}^{x_{1}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x} \cdot \left( \begin{array}{l}{1} \\ {0}\end{array}\right)+\int_{\mathrm{x}_{2}-\frac{\delta}{2}}^{\mathrm{x}_{2}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x} \cdot \left( \begin{array}{l}{0} \\ {1}\end{array}\right) \right]
\nonumber \]
\(\Psi^{ʹʹ}\)(p) is the projection of \(\Psi^{ʹ}\)(p) onto a diagonal polarizer \(\langle D |\).
\[
\Psi^{\prime \prime}(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \cdot \left( \begin{array}{l}{1} \\ {1}\end{array}\right)^{\mathrm{T}} \cdot \Psi^{\prime}(\mathrm{p})
\nonumber \]
\(\Psi^{ʹ'ʹ}\)(p) is the projection of \(\Psi^{ʹ}\)(p) onto a diagonal polarizer \(\langle A |\).
\[
\Psi^{\prime \prime \prime}(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \cdot \left( \begin{array}{c}{1} \\ {-1}\end{array}\right)^{\mathrm{T}} \cdot \Psi^{\prime}(\mathrm{p})
\nonumber \]
Rewriting \(\Psi^{ʹ}\)(p) in terms of \(|D\rangle\) and \(|A\rangle\) clearly shows the origin of the phase difference between the \(\left(|\Psi^{\prime \prime}(\mathrm{p})|\right)^{2}\) and \(\left(|\Psi^{\prime \prime \prime}(\mathrm{p})|\right)^{2}\) interference patterns.
\[
\Psi^{\prime}(p)=\left\langle p | \Psi^{\prime}\right\rangle=\frac{1}{2}\left[\left(\left\langle p | x_{1}\right\rangle+\left\langle p | x_{2}\right\rangle\right) | D\right\rangle+\left(\left\langle p | x_{1}\right\rangle-\left\langle p | x_{2}\right\rangle\right) | A \rangle ]
\nonumber \]

