9.22: Numerical Solutions for a Modified Harmonic Potential
- Page ID
- 137745
This tutorial deals with the following potential function:
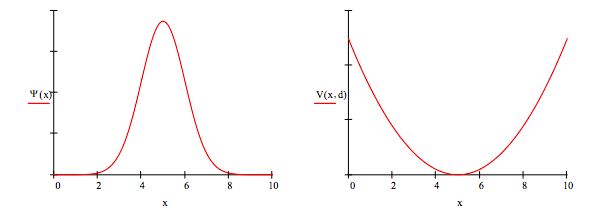
\[ V(x, d) = \bigg| _{ \infty ~otherwise}^{ \frac{1}{2} k(x-d)^2~if~x \geq 0 + d \leq 0} \nonumber \]
If d = 0 we have the harmonic oscillator on the half-line with eigenvalues 1.5, 3.5, 5.5, ... for k = \( \mu\) = 1. For large values of d we have the full harmonic oscillator problem displaced in the x-direction by d with eigenvalues 0.5, 1.5, 2.5, ... for k = \( \mu\) = 1. For small to intermediate values of d the potential can be used to model the interaction of an atom or molecule with a surface.
Integration limit: xmax = 10
Effective mass: \( \mu\) = 1
Force constant: k = 1
Potential energy minimum: d = 5
Potential energy:
\[ V(x,d) = \frac{k}{2} (x-d)^2 \nonumber \]
Integration algorithm:
Given
\[ \nonumber \]
Normalize wavefunction:
\[ \psi (x) = \frac{ \psi (x)}{ \sqrt{ \int_{0}^{x_{max}} \psi (x)^2 dx}} \nonumber \]
Energy guess: E = 0.5
Calculate average position:
\[ X_{avg} = \int_{0}^{x_{max}} \psi (x) x \psi (x) dx = 5 \nonumber \]
Calculate potential and kinetic energy:
\[ V_{avg} = \int_{0}^{x_{max}} \psi (x) V(x,d) \psi (x) dx = 0.25 \nonumber \]
\[ T_{avg} = E - V_{avg} = 0.25 \nonumber \]
Exercises:
- For d = 0, k = \( \mu\) = 1 confirm that the first three energy eigenvalues are 1.5, 3.5 and 5.5 Eh. Start with xmax = 5, but be prepared to adjust to larger values if necessary. xmax is effectively infinity.
- For d = 5, k = \( \mu\) = 1 confirm that the first three energy eigenvalues are 0.5, 1.5 and 2.5 Eh. Start with xmax = 10, but be prepared to adjust to larger values if necessary.
- Determine and compare the virial theorem for the exercises above.
- Calculate the probability that tunneling is occurring for the ground state for the first two exercises. (Answers: 0.112, 0.157)

