9.18: Particle in an Infinite Spherical Potential Well
- Page ID
- 137741
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Reduced mass: \( \mu\) = 1
Angular momentum: L = 2
Integration limit: rmax = 1
Solve Schrödinger's equation numerically. Use Mathcad's ODE solve block:
Given
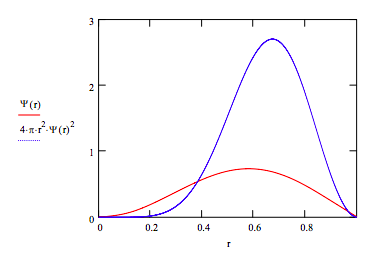
\[ \frac{-1}{2 \mu} \frac{d^2}{dr^2} \psi (r) - \frac{1}{r \mu} \frac{d}{dr} \psi (r) + \bigg[ \frac{L (L + 1)}{2 \mu r^2} \bigg] \psi (r) = E \psi (r)~~~ \psi (.0001) = .1~~~ \psi '(.0001) = 0 \nonumber \]
\[ \psi = Odesolve (r, r_{max}) \nonumber \]
Normalize the wavefunction:
\[ \psi (r) = \left( \int_{0}^{r_{max}} \psi (r)^2 4 \pi r^2 dr \right) ^{ \frac{-1}{2}} \psi (r) \nonumber \]
Energy guess: E = 16.51
r = 0, .001 .. rmax