9.17: Particle in a Box with Multiple Internal Barriers
- Page ID
- 137740
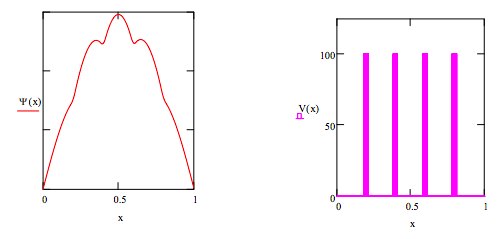
Integration limit: xmax = 1
Effective mass: \( \mu\) = 1
Barrier height: V0 = 100
Potential energy:
\[V(x) = \bigg|^{V_0~if~(x \geq .185)(x \leq .215) + (x \geq .385)(x \leq .415) + (x \geq .585) (x \leq .615) + (x \geq .785) (x \leq .815)}_{0~otherwise} \nonumber \]
Numerical integration of Schrödinger's equation:
Given
\[ \frac{-1}{2 \mu} \frac{d^2}{dx^2} \psi (x) + V(x) \psi (x) = E \psi (x) \nonumber \]
\[ \psi (0) = 0 \nonumber \]
\[ \psi ' (0) = 0.1 \nonumber \]
\[ \psi = Odesolve (x, x_{max} \nonumber \]
Normalize wave function:
\[ \psi (x) = \frac{ \psi (x)}{ \sqrt{ \int_{0}^{x_{max}} \psi (x)^2 dx}} \nonumber \]
Enter energy guess: E = 18.85
Calculate kinetic energy:
\[ T = \int_{0}^{1} \psi (x) \frac{-1}{2} \frac{d^2}{dx^2} \psi (x) dx = 5.926 \nonumber \]
Calculate potential energy:
\[ V = E - T = 12.924 \nonumber \]
Tunneling probability:
\[ \frac{V}{V_0} \times 100 = 12.924 \nonumber \]

