9.16: Another Look at the in a Box with an Internal Barrier

Last updated
Save as PDF

Page ID: 137737

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The purpose of this tutorial is to explore the impact of the presence of a large (100 E_h) thin (0.10 a₀) internal barrier on the solutions to the particle-in-a-box (PIB) problem. Schrödinger's equation is integrated numerically for the first five energy states. (Integration algorithm taken form J. C. Hansen, J. Chem. Educ. Software, 8C2, 1996.)

For the one-bohr PIB the energy eigenvalues are:

m = 1 .. 5

E_m = \( \frac{m^2 \pi^2}{2}\)

E^T = (4.935 19.739 44.413 78.957 123.37)

Set parameters:

n = 100

xmin = 0

xmax = 1

\( \Delta = \frac{xmax-xmin}{n-1}\)

\( \mu\) = 1

Vo = 100

lb = .45

rb = .55

Calculate position vector, the potential energy matrix, and the kinetic energy matrix. Then combine them into a total energy matrix.

i = 1 .. n j = 1 .. n x_i = xmin + (i - 1) \( \Delta\)

Potential energy:

\[ V_{i~j} = if[ (x_i \geq lb ) (x_i \leq rb ), Vo,~0] \nonumber \]

Kinetic energy:

\[ T_{i,~j} = if \bigg[ i=j, \frac{ \pi ^{2}}{6 \mu \Delta ^{2}}, \frac{ (-1)^{i-j}}{ (i-j)^{2} \mu \Delta^{2}} \bigg] \nonumber \]

\[ V_{i,~j} = if \bigg[ i =j,~ D \big[ 1 - exp \big[ - \beta (|x_i| - x_0) \big] \big] ^2 ,~0 \bigg] \nonumber \]

\[ T_{i,~j} = if \bigg[ i=j, \frac{ \pi ^{2}}{6 \mu \Delta ^{2}}, \frac{ (-1)^{i-j}}{ (i-j)^{2} \mu \Delta^{2}} \bigg] \nonumber \]

Hamiltonian matrix: H = T + V

Find eigenvalues: E = sort(eigenvals(H))

Display selected eigenvalues: m = 1 .. 5

E_m =

\( \begin{array}{|r|}
\hline \\
15.011 \\
\hline \\
19.589 \\
\hline \\
60.453 \\
\hline \\
78.268 \\
\hline \\
137.903 \\
\hline
\end{array} \)

Calculate selected eigenvectors:

k = 1 .. 4

\[ \psi (k) = eigenvec (H, E_k) \nonumber \]

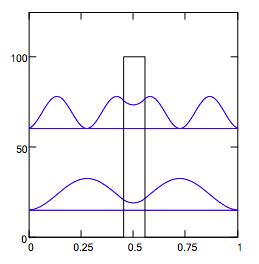
Display probability distributions and energy level manifold in the presence of the internal potential barrier:

n = 1 and n = 3 states:

Screen Shot 2019-02-19 at 11.11.58 AM.png

n = 2 and n = 4 states:

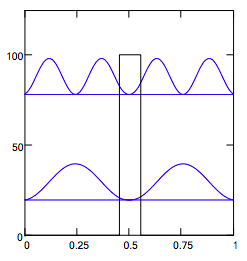
Screen Shot 2019-02-19 at 11.12.02 AM.png

It is clear from the numeric and graphic display of the energy manifold that the presence of the internal barrier causes a bunching of the energy eigenstates for the four lowest levels. This is frequently called "inversion doubling" because of an identical effect that appears in the analysis of the ammonia umbrella inversion. This gives the impression that a second set of quantized energy levels is created by the internal barrier. However, the correct explanation for this bunching is evident in the display of the four lowest wave functions. The presence of the barrier raises all energy levels relative to the simple PIB, but the n = 2 and n = 4 states have nodes in the barrier, thus reducing the barrier's effect on raising the energy. Thus the odd states are raised in energy more than the even states, causing the bunching.