9.13: Numerical Solutions for the Lennard-Jones Potential
- Page ID
- 137731
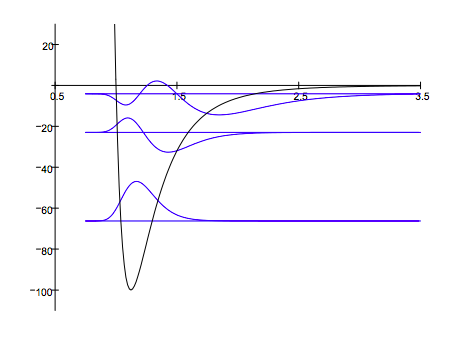
Merrill (Am. J. Phys. 1972, 40, 138) showed that a Lennard-Jones 6-12 potential with these parameters had three bound states. This is verified by numerical integration of Schrödinger's equation. The integration algorithm is taken from J. C. Hansen, J. Chem. Educ. Software, 8C2, 1996.
Set parameters:
- n = 200
- \(x_{min} = 0.75\)
- \(x_{max} = 3.5\)
- \(\Delta = \frac{xmax - xmin}{n-1}\)
- \( \mu\) = 1
- \( \sigma\) = 1
- \( \varepsilon\) = 100
Numerical integration algorithm:
i = 1 .. n j = 1 .. n xi = xmin + (i - 1) \( \Delta\)
\[ V_{i,~j} = if \bigg[ i =j,~4 \varepsilon \bigg[ \left( \frac{ \sigma}{x_i} \right)^12 - \left( \frac{ \sigma}{x_i} \right) ^6 \bigg] ,0~ \bigg] \nonumber \]
\[ T_{i,~j} = if \bigg[ i=j, \frac{ \pi ^{2}}{6 \mu \Delta ^{2}}, \frac{ (-1)^{i-j}}{ (i-j)^{2} \mu \Delta^{2}} \bigg] \nonumber \]
Hamiltonian matrix: H = T + V
Find eigenvalues: E = sort(eigenvals(H))
Display three eigenvalues: m = 1 .. 4
Em =
\( \begin{array}{|r|}
\hline \\
-66.269 \\
\hline \\
-22.981 \\
\hline \\
-4.132 \\
\hline \\
1.096 \\
\hline
\end{array} \)
Calculate eigenvectors:
k = 1 .. 3
\[ \psi (k) = eigenvec (H, E_k) \nonumber \]
Display results: