9.7: Particle in a Slanted Well Potential

Last updated
Save as PDF

Page ID: 135869

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Numerical Solutions for Schrödinger's Equation for the Particle in the Slanted Box

Parameters go here: \( x_{max} = 1\) \( \mu = 1\) \( V_{0} = 2\)

Potential energy \( V(x) = V_{0} x\)

Given

\[ \frac{-1}{2 \mu} \frac{d^{2}}{dx^{2}} \psi (x) + V(x) \psi (x) = E \psi (x) \nonumber \]

with these boundary conditions: \( \psi (0) = 0\) and \( \psi '(0) = 0.1\)

\( \psi = Odesolve(x, x_{max})\) Normalize wavefunction: \( \psi (x) = \frac{ \psi (x)}{ \sqrt{ \int_{0}^{x_{max}} \psi (x)^{2} dx}}\)

Enter energy guess: E = 5.925

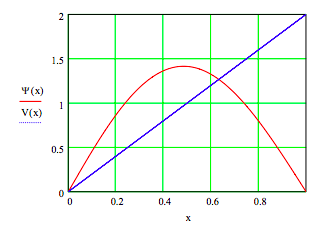
Screen Shot 2019-02-06 at 7.03.20 PM.png

Calculate most probably position: x = 0.5 Given \( \frac{d}{dx} \psi (x) = 0\) Find (x) = 0.485

Calculate average position: \( X_{avg} = \int_{0}^{1} \psi (x) (x) \psi (x) dx\) \( X_{avg} = 0.491\)

Calculate potential and kinetic energy:

\( V_{avg} = V_{0} X_{avg}\) \( V_{avg} = 0.983\)

\( T_{avg} = E - V_{avg}\) \( T_{avg} = 4.942\)