9.3: Particle in a Gravitational Field
- Page ID
- 135865
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
The Unhindered Quantized Bouncing Particle
- Integration limit: \( z_{max} = 3\)
- Mass: \( m = 2\)
- Acceleration due to gravity: \(g = 1\)
The first 10 roots of the Airy function are as follows:
| a1 = 2.33810 | a2 = 4.08794 | a3 = 5.52055 | a4 = 6.78670 | a5 = 7.94413 |
| a6 = 8.02265 | a7 = 10.04017 | a8 = 11.00852 | a9 = 11.93601 | a10 = 12.82877 |
Calculate energy analytically by selecting the appropriate Airy function root:
i = 1 E = \( \frac{mg^{2}}{2}^{ \frac{1}{3}} a_{1}\) E = 2.338
Generate the associated wavefunction numerically: Potential energy: \(V(z) = mgz\)
Given \( \frac{-1}{2 \cdot m} \frac{d^{2}}{dz^{2}} \psi (z) + V (z) \psi (z) \equiv E \psi (z)\)
\( \psi (0.0) = 0.0\)
\( \psi '(0.0) = 0.1\)
Given, \( \psi = Odesolve (z, z_{max})\)
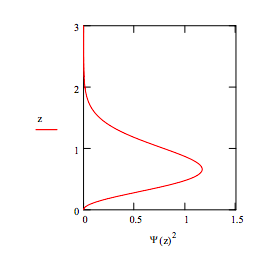
Normalize wavefunction: \( \psi (z) = \frac{ \psi (z)}{ \sqrt{ \int_{0}^{z_{max}} \psi (z)^{2} dz}}\)