9.2: Particle in an Infinite Potential Well
- Page ID
- 135864
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Numerical Solutions for Schrödinger's Equation
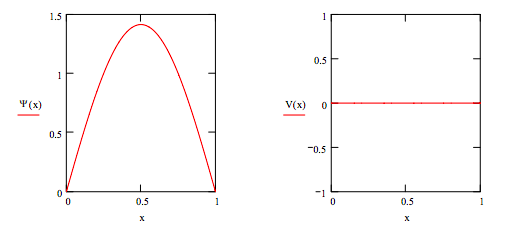
Integration limit: xmax := 1 Effective mass: \( \mu\) := 1
Potential energy: V(x) := 0
Numerical integration of Schrödinger's equation:
Given: \( \frac{1}{2 \mu} \frac{d^{2}}{dx^{2}} \Psi (x) + V(x) \Psi (x) = E \Psi (x)\) \( \Psi (0) = 0\) \( \Psi '(0) = 0.1\)
\( \Psi := Odesolve (x, x_{max}\) Normalize wave function: \( \Psi (x) := \frac{ \Psi (x)}{ \sqrt{ \int_{0}^{x_{max}}} \Psi (x)^{2}dx}\)
Enter energy guess: E = 4.934
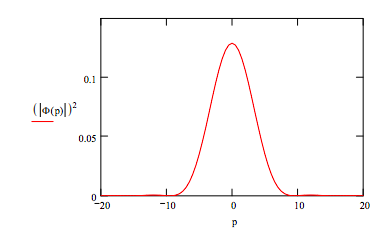
Fourier transform coordinate wave function into momentum space:
p := -20, -19.5 .. 20
\( \Phi (p) := \frac{1}{2 \mu} \int_{0}^{x_{max}} exp(-i \cdot p \cdot x) \cdot \Psi (x) dx\)