9.22: Numerical Solutions for a Modified Harmonic Potential

Last updated
Save as PDF

Page ID: 137745

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

This tutorial deals with the following potential function:

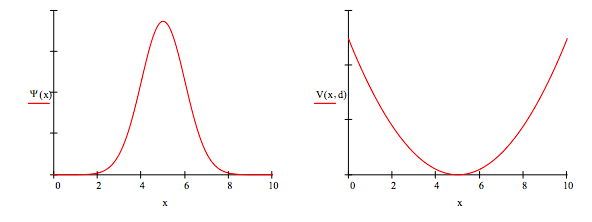
\[ V(x, d) = \bigg| _{ \infty ~otherwise}^{ \frac{1}{2} k(x-d)^2~if~x \geq 0 + d \leq 0} \nonumber \]

If d = 0 we have the harmonic oscillator on the half-line with eigenvalues 1.5, 3.5, 5.5, ... for k = \( \mu\) = 1. For large values of d we have the full harmonic oscillator problem displaced in the x-direction by d with eigenvalues 0.5, 1.5, 2.5, ... for k = \( \mu\) = 1. For small to intermediate values of d the potential can be used to model the interaction of an atom or molecule with a surface.

Integration limit: x_max = 10

Effective mass: \( \mu\) = 1

Force constant: k = 1

Potential energy minimum: d = 5

Potential energy:

\[ V(x,d) = \frac{k}{2} (x-d)^2 \nonumber \]

Integration algorithm:

Given

\[ \nonumber \]

Normalize wavefunction:

\[ \psi (x) = \frac{ \psi (x)}{ \sqrt{ \int_{0}^{x_{max}} \psi (x)^2 dx}} \nonumber \]

Energy guess: E = 0.5

Screen Shot 2019-02-19 at 12.16.32 PM.png

Calculate average position:

\[ X_{avg} = \int_{0}^{x_{max}} \psi (x) x \psi (x) dx = 5 \nonumber \]

Calculate potential and kinetic energy:

\[ V_{avg} = \int_{0}^{x_{max}} \psi (x) V(x,d) \psi (x) dx = 0.25 \nonumber \]

\[ T_{avg} = E - V_{avg} = 0.25 \nonumber \]

Exercises:

For d = 0, k = \( \mu\) = 1 confirm that the first three energy eigenvalues are 1.5, 3.5 and 5.5 E_h. Start with x_max = 5, but be prepared to adjust to larger values if necessary. xmax is effectively infinity.
For d = 5, k = \( \mu\) = 1 confirm that the first three energy eigenvalues are 0.5, 1.5 and 2.5 Eh. Start with x_max = 10, but be prepared to adjust to larger values if necessary.
Determine and compare the virial theorem for the exercises above.
Calculate the probability that tunneling is occurring for the ground state for the first two exercises. (Answers: 0.112, 0.157)