Skip to main content
Chemistry LibreTexts

11.17: The Origin of KE = 3/2 RT

  1. Last updated
  2. Save as PDF
  • Page ID
    135513

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    The Kinetic Molecular Theory of Gases

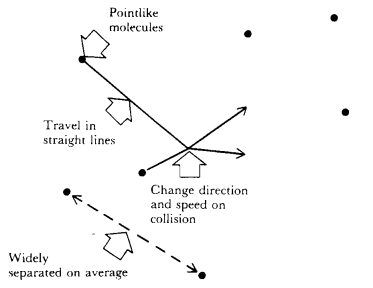
    A gas consists of a collection of molecules in continuous random motion with varying speed.

    The individual gas molecules are extremely small when compared with the volume of the container they occupy.

    The molecules move in straight lines until they collide with each other or the walls of the container.

    The molecules do not interact with each other or the walls of the container except during these collisions.

    The laws of classical physics can be used to analyze the motion of the gas molecules and to calculate the bulk properties of the gas.

    The basic features of the kinetic molecular theory (KMT) are illustrated in the figure below.

    Screen Shot 2019-02-05 at 1.47.16 PM.png

    When the KMT is used to calculate the pressure of a gas the following expression results

    \[ P = \frac{ \frac{1}{3} nMV^{2}}{V} \nonumber \]

    where n is the number of moles of gas, M is the molar mass of the gas, v2 is the average of the velocity squared, and V is the volume of the container.

    The ideal gas law summarizes the behavior of gases with respect to the macroscopic variables of temperature, pressure, volume and moles of gas.

    \[ P = \frac{nRT}{V} \nonumber \]

    A comparison of equations (1) and (2), that is, a comparison between the results of a theoretical analysis using the KMT and the actual experimental behavior of gases reveals that

    \[ \frac{1}{2} Mv^{2} = \frac{3}{2}RT \nonumber \]

    Thus, the proportionality of the average molecular kinetic energy to the absolute temperature is a conclusion drawn by comparing a theoretical expression with an empirical equation which summarizes macroscopic gas facts.

    The resulting equation, (3), provides an interpretation of temperature in terms of molecular motion.

    This page titled 11.17: The Origin of KE = 3/2 RT is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Frank Rioux via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.