11.6: An Alternative Derivation of Gas Pressure Using the Kinetic Theory
- Page ID
- 134864
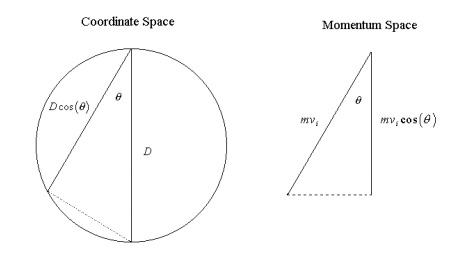
General chemistry and physical chemistry texts that use the kinetic theory to derive the pressure of an ideal gas do so by studying a gas in a cubic or rectangular container (1). The purpose of this note is to outline this derivation for a gas in a spherical container. A visual representation of this approach in coordinate and momentum space is provided in the accompanying figure.
A sphere of diameter \(D\) contains gas molecules moving randomly, executing elastic collisions with each other and the surface of the container as postulated by the kinetic theory. Consider a molecule labeled i of mass m and velocity vi making a collision with the surface at an angle 2 relative to the perpendicular to the surface. The momentum transferred to the container in the direction perpendicular to the surface by the collision is
\[\Delta (m\nu )_{surf}=2m\nu _{i}\cos(\Theta ) \nonumber \]
Because the molecule travels a distance between \(Dcos(\Theta )\) collisions with the surface, the time interval between collisions is
\[\Delta t=\frac{D\cos(\Theta )}{v_{i}} \nonumber \]
The force (F) exerted on the surface is the rate of momentum transfer,
\[F_{i}=\dfrac{\Delta (m\nu )_{surf}}{\Delta t}=\dfrac{2mv_{i}^{2}}{D} \nonumber \]
Pressure (P) is force divided by area (A) and the surface area of a sphere is \(\pi D^{2}\). The volume of a sphere (V) is \(\frac{1}{6}\pi D^{3}\), therefore
\[P_{i}=\dfrac{F_{i}}{A}=\dfrac{2mv_{i}^{2}}{\pi D^{3}}=\frac{mv_{i}^{2}}{3V} \nonumber \]
For a mole of gas molecules the total pressure is
\[P=\sum_{i}^{N_{A}}P_{i}=\frac{m}{3V}\sum_{i}^{N_{A}}v^{2}_{i}=\frac{M \big \langle v^{2} \big \rangle}{3V}=\frac{3 \big \langle KE \big \rangle}{3V} \nonumber \]
where \( \big \langle v^{2} \big \rangle =\frac{1}{N_{A}}\sum_{i}^{N_{A}}v^{2}_{i}\) and \(M=N_{A}m\).
As Dewey Carpenter pointed out many years ago (2), it is through a comparison of equation (5) with the ideal gas law that we conclude that the average molar kinetic energy of a gas is proportional to its absolute temperature.
\[ \big \langle KE \big \rangle = \frac{1}{2}M \big \langle v^{2} \big \rangle=\frac{3}{2}RT \nonumber \]
Unfortunately most introductory texts incorrectly include this result as a postulate of the kinetic theory (3). With regard to the formal assumptions of the kinetic theory Carpenter noted (2), “No reference is made in these postulates to the property of temperature. This is because the kinetic theory is a purely mechanical theory, whereas the concept of temperature belongs to the discipline of thermodynamics.”
References
- See for example: Zumdahl, S. S.; Zumdahl, S. A. Chemistry, 5th ed.; Houghton Mifflin Co.: Boston, 2000; pp A14-A16. Atkins, P. W. Physical Chemistry, 6th ed., W. H. Freeman and Co., New York, 1998, pp 23-25.
- Carpenter, D. K. J. Chem. Educ. 1966, 43, 332.
- A survey of 15 currently available general chemistry textbooks revealed that ten included equation (6), or some form of it, as an assumption of the kinetic theory.