5.23: Crystal Structure, Rotational Symmetry, and Quasicrystals

Prior to 1991 crystals were defined to be solids having only 2-, 3-, 4- and 6-fold rotational symmetry because only these rotational symmetries have the required translational periodicity to build the long-range order of a crystalline solid. Long-range order is synonymous with periodicity, requiring some unit structure which repeats itself by translation in all directions infinitely. It is easy to demonstrate that a pentagon, with 5-fold rotational symmetry cannot be used as a unit cell to create long-range order in a plane or in three-dimensions.

The justification for this definition was that solid structures with 2-, 3-, 4- and 6-fold rotational symmetry yield discrete diffraction patterns that also have translational periodicity. Another way to put this is to say that solid structures with 2-, 3-, 4- and 6-fold rotational symmetry have reciprocal lattices that also have translational periodicity. Yet, another way to put this, of course, is that the Fourier transforms of geometries with 2-, 3-, 4- and 6-fold rotational symmetry yield lattice-like momentum distributions with translational periodicity. This latter statement is preferred by the author because it emphasizes that diffraction patterns are actually the momentum distributions of the diffracted particles.

The key in this latter interpretation is that diffraction experiments involve an initial spatial localization of the radiation through interaction with the crystal lattice, followed as required by the uncertainty principle, a delocalization of the momentum distribution in the detection plane.

Let’s look at some examples. First we examine the Fourier transforms of two mini-lattices with two- and three-fold rotational symmetry.

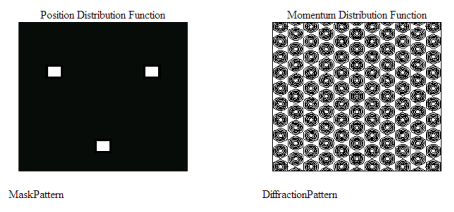
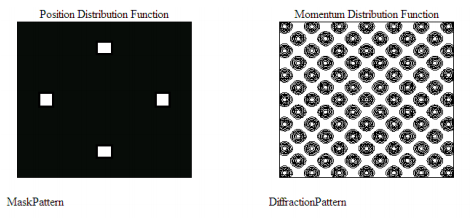
Clearly both diffraction patterns exhibit translational periodicity, their repeating units being a 90 degree rotation of the spatial structure. Next we look at four-fold rotational symmetry and see that the unit cell is obvious.

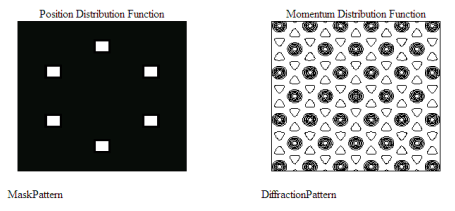
Six-fold rotational symmetry is more interesting than the previous three examples, but again the unit cell is easy to find.

Now look at what happens when we consider 5-fold symmetry – the diffraction pattern generated by a pentagon.

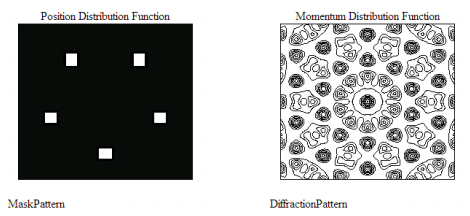
The unit cell, the universal repeating unit, is gone. The diffraction pattern is well-defined, it has rotational symmetry and it is appealing, but it does not satisfy the criterion for translational periodicity. That’s why 5-fold rotational symmetry is excluded from the list of symmetries that can generate diffraction patterns that have translational periodicity, and why by definition crystalline solids are not supposed to have 5-fold axes, or rotational axes greater than order six.

However, in 1984 an international research team consisting of D. Shechtman, I. Blech, D. Gratias and J. W. Cahn, published “Metallic phase with long-range orientational order and no translational symmetry” in Physical Review Letters 53, 1951-1953 (1984). The crystalline metallic phases they studied produced discrete diffraction patterns that were characteristic of the 5- and 10-fold rotational symmetry axes that were prohibited by the accepted definition of a crystalline solid.

In the face of this contradictory evidence, 5-fold rotational symmetry and a well-defined diffraction pattern, the International Union of Crystallography in 1991 redefined crystal to mean any solid having a discrete diffraction pattern. However, the solid phases discovered by Shechtman and his co-workers go by the name quasicrystals, indicating that they don’t quite have the same stature as those that don’t violate the rotational symmetry rule.