5.19: A Quantum Mechanical Interpretation of Diffraction

Last updated
Save as PDF

Page ID: 150544

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Diffraction has a simple quantum mechanical interpretation based on the uncertianty principle. Or we could say diffraction is an excellent way to illustrate the uncertainty principle.

A screen with a single slit of width, w, is illuminated with a coherent photon or particle beam. The normalized coordinate‐space wave function at the slit screen is,

\[ \Psi (x,~w) = \left| \begin{matrix} \frac{1}{ \sqrt{w}} \text{if} \left( x \geq - \frac{w}{2} \right) \left( x \leq \frac{w}{2} \right) \\ 0 \text{ otherwise} \end{matrix} \right. \nonumber \]

The coordinate‐space probability density, |Ψ(x,w)|², is displayed for a slit of unit width below

Screen Shot 2019-05-09 at 8.06.06 PM.png

The slit‐screen measures position, it localizes the incident beam in the x‐direction. According to the uncertainty principle, because position and momentum are complementary, or conjugate, observables, this measurement must be accompanied by a delocalization of the x‐component of the momentum. This can be seen by a Fourier transform of Ψ(x,w) into momentum space to obtain the momentum wave function, Φ(p_x,w).

\[ \Phi (p_x,~w) = \frac{1}{ \sqrt{2 \pi}} \int_{ - \frac{w}{2}}^{ \frac{w}{2}} exp ( -i p_x x) \frac{1}{w} dx \text{ simplify} \rightarrow \frac{ \sqrt{2} \sin \left( \frac{p_x w}{2}}{ \sqrt{ \pi} p_x \sqrt{w}} \nonumber \]

It is the momentum distribution, |Ψ(px ,w)|², shown below that is projected onto the detection screen. Thus, a position measurement at the detection screen is also effectively a measure of the x‐component of the particle momentum.

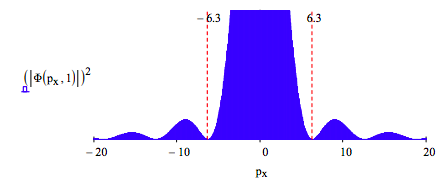
Screen Shot 2019-05-09 at 8.09.08 PM.png

In this figure we see the spread in momentum required by the uncertainty principle, plus interference fringes due to the fact that the incident beam can imerge from any where within the slit, allowing for constructive and destructive interference at the detection screen. If the slit width is decreased the position is more precisely known and the uncertainty principle demands a broadening in the momentum distribution as shown below.

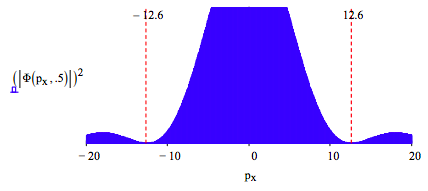
Equating uncertainty in position with slit width and uncertainty in momentum with the width of the intense center of the diffraction pattern, we have in atomic units: ΔxΔp_x = 12.6. If the slit width is decreased the position is more precisely known and the uncertainty principle demands a broadening in the momentum distribution as shown below. For slit width 0.5 we again find the product of the uncertainties is 12.6.

Screen Shot 2019-05-09 at 8.09.50 PM.png

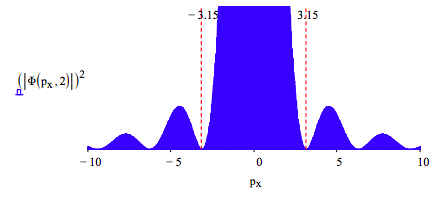
Naturally if the slit width is increased to 2.0 the position uncertainty increases and the uncertainty in momentum decreases yielding again ΔxΔp_x = 12.6.

Screen Shot 2019-05-09 at 8.09.58 PM.png

The x‐direction momentum can be expressed in terms of the wavelength of the illuminating beam and the diffraction angle using the following sequence of equations of which the second is the de Broglie relation in atomic units (h = 2π).

\[ \begin{matrix} p_x = p \sin ( \Theta) & p = \frac{2 \pi}{ \lambda} & p_x = \frac{2 \pi}{ \lambda} \sin ( \Theta) \end{matrix} \nonumber \]

\[ \Phi ( \Theta_x,~w,~ \lambda) = \sqrt{ \frac{2}{ \pi w}} \frac{ \sin \left( \frac{ \pi w}{ \lambda} \sin ( \Theta_w ) \right)}{ \frac{2 \pi}{ \lambda} \sin ( \Theta_w )} \nonumber \]

This allows one to explore the effect of the wavelength of the illuminating beam on the diffraction pattern. The figure below shows that a short wavelength (high momentum) illuminating beam gives rise to a narrower diffraction pattern.

Screen Shot 2019-05-09 at 8.10.06 PM.png

The method used here to calculate single‐slit diffraction patterns (momentum‐space distribution functions) is easily extended to multiple slits, and also to diffraction at two‐dimensional masks with a variety of hole geometries.

Primary source: ʺQuantum interference with slits,ʺ Thomas Marcella which appeared in European Journal of Physics 23, 615‐621 (2002).

See also: "Calculating diffraction patterns,ʺ F. Rioux in European Journal of Physics, 24, N1‐N3 (2003). ʺSingle‐slit Diffraction and the Uncertainty Principle,ʺ F. Rioux in Journal of Chemical Education, 82, 1210 (2005).

ʺExperimental verification of the Heisenberg uncertainty principle for hot fullerene moleculesʺ, O. Nairz, M. Arndt, and A. Zeilinger, Phys. Rev. A, 65, 032109 (2002).

ʺIntroducing the Uncertainty Principle Using Diffraction of Light Waves,ʺ Pedro L. Muino, Journal of Chemical Education, 77, 1025‐1027 (2000).