5.8: Is a Two-dimensional Fibonacci Array a Quasilattice?

Last updated
Save as PDF

Page ID: 150523

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

A two-dimensional Fibonacci lattice lacks translational periodicity but has a discrete diffraction pattern, just like a quasicrystal. However, it does not fit the definition of a quasilattice because it does not posses one of the 'forbidden' n-fold rotational symmetries (n = 5 or greater than 6) that are characteristic of quasicrystals and incompatible with translational periodicity. R. Lifshitz1, therefore, recommends that the symmetry requirement be relaxed so that two- and three-dimensional Fibonacci lattices can have quasilattice stature.

A one-dimensional Fibonacci grid consists of a sequence of long (L) and short (S) segments such as LSLLSLSLLS.... with L/S = 1.618, the golden ratio. A two-dimensional array is created by superimposing two such grids at a 90^o angle and placing atomic scatterers at the vertices.

\[ \begin{matrix} \text{Dimension of grid:} & A = 10 & m = 1 .. A & n = 1 .. A & \tau = \frac{1 + \sqrt{5}}{2} \end{matrix} \nonumber \]

Calculate the coordinates of the Fibonacci vertices in a two-dimensional lattice (see Lifshitz).

\[ \begin{matrix} x_m = \text{floor} \left( \frac{m}{ \tau} \right) \tau + \left( m - \text{floor} \left( \frac{m}{ \tau} \right) \right) -1 & y_n = \text{floor} \left( \frac{n}{ \tau} \right) \tau + \left( n - \text{floor} \left( \frac{n}{ \tau} \right) \right) - 1 \end{matrix} \nonumber \]

\[ \begin{matrix} x^T = \begin{pmatrix} 0 & 1.618 & 2.618 & 4.236 & 5.854 & 6.854 & 8.472 & 9.472 & 11.09 & 12.708 \end{pmatrix} \\ y^T = \begin{pmatrix} 0 & 1.618 & 2.618 & 4.236 & 5.854 & 6.854 & 8.472 & 9.472 & 11.09 & 12.708 \end{pmatrix} \end{matrix} \nonumber \]

Display the two-dimensional Fibonacci array:

2D Fibonacci Lattice

\[ \begin{matrix} \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \end{matrix} \nonumber \]

The diffraction pattern is the Fourier transform of the spatial Fibonacci array into the momentum representation.

Calculate momentum-space wave function:

\[ \Phi (p_x,~p_y) = \frac{1}{2 \pi} \sum_{m = 1}^A exp (-i p_x x_m) \sum_{n = 1}^A exp ( -i p_y y_n) \nonumber \]

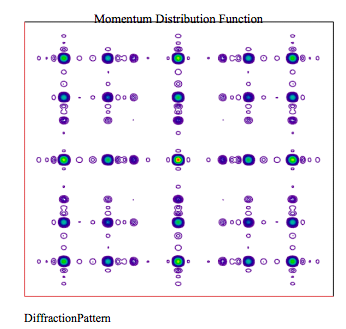
Display momentum-space distribution function (diffraction pattern).

\[ \begin{matrix} \Delta = 10 & N = 200 & j = 1 .. N & px_j = - \Delta + \frac{2 \Delta j}{N} & k = 1 .. N & py_k = - \Delta + \frac{2 \Delta k}{N} \end{matrix} \nonumber \]

\[ \text{Diffraction Pattern}_{j,~k} = \left( \left| \Phi (px_j,~py_k ) \right| \right)^2 \nonumber \]

Screen Shot 2019-05-08 at 2.20.31 PM.png

R. Lifshitz, "The square Fibonacci tiling," Journal of Alloys and Compounds 342, 186-190 (2002).