3.33: A Numerical Huckel Calculation on C10H8 Isomers

Last updated
Save as PDF

Page ID: 154840

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The numeric version of the Huckel molecular orbital theory (HMOT) is based on a connectivity matrix which records which atoms are bonded to each other. The eigenvalues of this matrix provide the HMOT energy levels and the HMOT wave functions.

The purpose of this exercise is to see what HMOT has to say about the relative stability of the C₁₀H₈ isomers shown below.

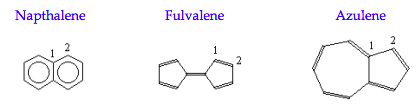
Screen Shot 2019-06-04 at 2.00.30 PM.png

Napthalene calculation: \( \begin{matrix} \text{Natoms = 10} & \text{Nocc = 5} \end{matrix}\)

\[ H = \begin{pmatrix} 0&1&0&0&0&1&0&0&0&1 \\ 1&0&1&0&0&0&0&0&0&0 \\ 0&1&0&1&0&0&0&0&0&0 \\ 0&0&1&0&1&0&0&0&0&0 \\ 0&0&0&1&0&1&0&0&0&0 \\ 1&0&0&0&1&0&1&0&0&0 \\ 0&0&0&0&0&1&0&1&0&0 \\ 0&0&0&0&0&0&1&0&1&0 \\ 0&0&0&0&0&0&0&1&0&1 \\ 1&0&0&0&0&0&0&0&1&0 \end{pmatrix} \nonumber \]

Calculate the eigenvalues and eigenvectors: \( \begin{matrix} \text{E = eigenvals(H)} & \text{E = sort(E)} \end{matrix}\)

\[ E^T = \begin{pmatrix} -2.303 & -1.618 & -1.303 & -1 & -0.618 & 0.618 & 1 & 1.303 & 1.618 & 2.303 \end{pmatrix} \nonumber \]

Calculate total π-electronic energy: \( \begin{matrix} E_{ \pi} = 2 \sum_{i = 1}^{ \text{Nocc}} E_i & E_{ \pi} = -13.683 \end{matrix}\)

Calculate the delocalization energy: \( \begin{matrix} E_{deloc} = E_{ \pi} + 2 \text{Nocc} & E_{deloc} = -3.683 \end{matrix}\)

Calculate the delocalization energy per atom: \( \frac{E_{deloc}}{Natoms} = -0.368\)

Fulvalene calculation:

\[ H = \begin{pmatrix} 0&1&0&0&1&0&0&0&0&0 \\ 1&0&1&0&0&0&0&0&0&0 \\ 0&1&0&1&0&0&0&0&0&0 \\ 0&0&1&0&1&0&0&0&0&0 \\ 1&0&0&1&0&1&0&0&0&0 \\ 0&0&0&0&1&0&1&0&0&1 \\ 0&0&0&0&0&1&0&1&0&0 \\ 0&0&0&0&0&0&1&0&1&0 \\ 0&0&0&0&0&0&0&1&0&1 \\ 0&0&0&0&0&1&0&0&1&0 \end{pmatrix} \nonumber \]

Calculate the eigenvalues and eigenvectors: \( \begin{matrix} \text{E = eigenvals(H)} & \text{E = sort(E)} \end{matrix}\)

\[ E^T = \begin{pmatrix} -2.115 & -1.618 & -1.618 & -1.303 & 0.254 & 0.618 & 0.618 & 1 & 1.861 & 2.303 \end{pmatrix} \nonumber \]

Calculate the total π-electronic energy: \( \begin{matrix} E_{ \pi} = 2 \sum_{i = 1}^{ \text{Nocc}} E_i & E_{ \pi} = -12.799 \end{matrix}\)

Calculate the delocalization energy: \( \begin{matrix} E_{ \text{deloc}} = E_{ \pi} + 2 \text{Nocc} & E_{ deloc} = -2.799 \end{matrix}\)

Calculate the delocalization energy per atom: \( \frac{E_{deloc}}{Natoms} = -0.28\)

Azulene calculation:

\[ H = \begin{pmatrix} 0&1&0&0&1&0&0&0&0&1 \\ 1&0&1&0&0&0&0&0&0&0 \\ 0&1&0&1&0&0&0&0&0&0 \\ 0&0&1&0&1&0&0&0&0&0 \\ 1&0&0&1&0&1&0&0&0&0 \\ 0&0&0&0&1&0&1&0&0&0 \\ 0&0&0&0&0&1&0&1&0&0 \\ 0&0&0&0&0&0&1&0&1&0 \\ 0&0&0&0&0&0&0&1&0&1 \\ 1&0&0&0&0&0&0&0&1&0 \end{pmatrix} \nonumber \]

Calculate the eigenvalues and eigenvectors: \( \begin{matrix} \text{E = eigenvals(H)} & \text{E = sort(E)} \end{matrix}\)

Calculate the total π-electronic energy: \( \begin{matrix} E_{ \pi} = 2 \sum_{i = 1}^{ \text{Nocc}} E_i & E_{ \pi} = -13.364 \end{matrix}\)

Calculate the delocalization energy per atom: \( \frac{E_{deloc}}{Natoms} = -0.336\)

The HMOT calculations indicate that napthalene has the largest delocalization energy and fulvalene has the smallest delocalization energy.

\[ \begin{pmatrix} \text{Molecule} & E_{ \pi} & E_{deloc} & \frac{E_{deloc}}{atom} \\ \text{Napthalene} & -13.683 & -3.683 & -0.368 \\ \text{Azulene} & -13.364 & -3.364 & -0.336 \\ \text{Fulvalene} & -12.799 & -2.799 & -0.280 \end{pmatrix} \nonumber \]

The enthalpies of formation are available for napthalene and azulene and are 150 and 280 kJ/mol, respectively. Thus the rudimentary Huckel calculation is consistent with the thermodynamic data.