3.30: Chemical Bonding and Electronic Structure of Buckminsterfullerene

As is well-known C₆₀ resembles an American soccerball, containing 12 pentagons and 20 hexagons (see Figure 1). Removing the leather, but keeping the seams, leaves 60 vertices for the carbon atoms and 90 covalent bonds between them, 60 single bonds and 30 double bonds.

Figure 2. Curly and Smalley (see Scientific American, October 1991, pp 54-63) have described it as the "roundest molecule that can possible exist."

Figure 1.

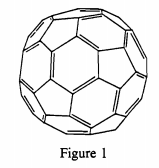
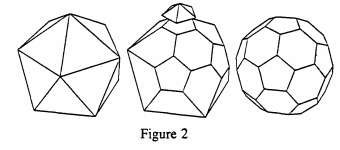
However, we should note that the actual bonding in C60 is somewhat more complex. The reason for this is that sp² hybrid orbitals all lie in the same plane, but inspection of any model of buckminsterfullerene clearly shows that the environment at each carbon is not planar. So the hybridization at each carbon cannot be pure sp², and current research indicates that the actual hybridization is sp^2.3. Since we are trying to develop a simple, but serviceable, model of the bonding and electronic structure of C₆₀, we will assume sp² hybridization as a first approximation. It might be a good idea at this point to review what Zumdahl has to say about models on pages 362 to 364 in his textbook.

In chapter 8 we spent a fair amount of time drawing resonance structures for molecules and ions that had more than one correct Lewis structure. C₆₀ is such a molecule and, as a matter of fact, it has 12,500 resonance structures! Try drawing at least two resonance structures, one in which all double bonds are in the hexagons, and one in which the pentagons have double bonds.

Associated with the concept of resonance is the idea of delocalization of electrons. For example, for a molecule with two resonance structures of equal plausibility (review formal charge arguments) we would say that the molecule's electronic structure is not correctly represented by either one or the other, but an average of the two (see Zumdahl's discussion of resonance in section 8.12). The fact that more than one Lewis structure can be written for a molecule is an indication of weakness in the Lewis' localized electron pair model of chemical bonding, because the existence of resonance structures actually delocalizes the r-electrons over the molecule as a whole. Benzene is, perhaps, the best example of this. Rather than writing structures A or B below, we write C and think Figure 9.48b in Zumdahl.

Since C₆₀ has 12,500 resonance structures involving its 60 r-electrons we may profitably consider the r-electrons to be particles delocalized over a sphere. The solution of Schrödinger's equation for a particle on a sphere is well known. Since a particle on a sphere is restricted to move in two directions, in spherical polar coordinates its position can be described by two angles, θ and ϕ. Thus, two spatial quantum numbers are required and they are the old familiar 1 and m₁ of Chapter 7 of Zumdahl. Since the particles in question are electrons, the spin quantum number, m_s, is also required. The rules for the quantum numbers are as stated in Chapter 7: 1 can have integer values starting with 0; m₁ can have integer values ranging from -1 to +1; m_s, can have the values of ±1/2.

Using the rules for the 1 and m₁ quantum numbers makes it possible to construct an energy level diagram for an electron on a sphere. This is shown in Figure 4.

Figure 5.

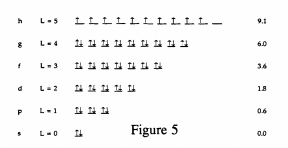
This figure shows 10 unpaired electrons (Hund's Rule) in the highest occupied energy level. This would suggest that C₆₀ is paramagnetic and perhaps a conductor of electricity. In fact C₆₀ is diamagnetic (no unpaired electrons) and does not conduct electricity. Thus, this initial model for the bonding and electronic structure of C₆₀ is not correct.

A way out of this difficulty is to recall that C₆₀ is not a sphere, but a truncated iscosohedron. The symmetry of the truncated icosohedron is high, but not as high as a perfect sphere. The main consequence of this is that the degeneracies of some of the higher energy levels are split by the lower iscosahedral symmetry. You will see more of this in CHEM 234 when we study transition metal complexes and crystal field theory. Figure 6 shows what happens to the energy levels under icosahedral symmetry and how they are filled with 60 electrons.

Note that this energy level diagram is in agreement with the basic facts about C₆₀. It is a non-conductor and diamagnetic. In addition, it suggests that C₆₀ might have a fairly high electron affinity because it has a low-lying unoccupied energy level with room for six electrons. This is consistent with the fact that K₃C₆₀ is known and is a conductor and passes into a super-conducting state at low temperature. The electro-positive potassium atoms supply three electrons which half-fill the lowest unoccupied energy level. K₆C₆₀ is also known and is a non-conductor. This too is consistent with the model as the potassiums supply six valence electrons completely filling the C₆₀'s lowest unoccupied energy level.

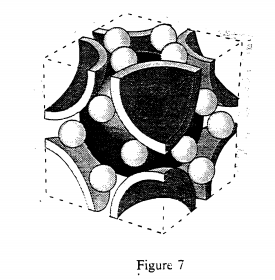
In Chapter 10 we will see that the crystal structures of solid C₆₀, K₃C₆₀, and K₆C₆₀ can be described using the same concepts as are used to describe the more familiar structures of NaCl, CsCl₂, and CaF₂. For now we can say, for example, that solid buckminsterfullerene consists of a face-centered cubic packing of spherical C₆₀ molecules (see Figures 10.15 and 10.17 in Zumdahl). K₃C₆₀ can be described as face-centered cubic C₆₀^3- ions with K⁺ ions in all the tetrahedral and octahedral holes (see Figure 10.33 in Zumdahl for an illustration of tetrahedral and octahedral holes). You should confirm that this structure gives the correct stoichiometric ratios for the ions. By contrast K₆C₆₀ is body centered C₆₀^3- ions with four K⁺ ions in each of the six cube faces as shown in Figure 7 below. Again you should confirm that this structure gives the correct ratio of the stoichiometric coefficients.

While it is not possible to go into detail at this point, it is also the case that the model presented here for the bonding and electronic structure of buckminsterfullerene is consistent with the absorption spectra of C₆₀ in the ultraviolet, visible, and infrared regions of the electromagnetic spectrum.