3.24: Another Critique of VSEPR

Gillespie's Valence Shell Electron Pair Repulsion (VSEPR) theory holds that the configuration of valence electron pairs surrounding a central nonvalence nuclear kernel is determined by minimization of electron-electron potential energy. The following summary statement by Gillespie is taken from J. Chem. Educ. 40, 295 (1963).

The theory proposes that the stereochemistry of an atom is determined primarily by the repulsive interactions between the electron pairs in a valence shell. The electrons in a valence shell are regarded as occupying essentially localized orbitals that are oriented in space around the nucleus and completed inner electron shells (nuclear kernel) so that their average distance apart is maximized. The tendency of electrons in a pair in a valence-shell to adopt an arrangement which maximizes their distance apart may be regarded as arising from repulsive interactions between the electron pairs.

However, quantum theory teaches that minimization of the total energy determines electronic structure. The following analysis will show that the VSEPR short-cut is specious; electron-nucleus attraction is the most important factor in determining electronic geometry and electron-electron repulsion actually increases in the transition from square planar to the more stable tetrahedral geometry in the system examined. If VSEPR gets the right answer, it does so for the wrong reason.

For the sake of mathematical simplicity the calculation of the total energy of an atomic configuration of charges will be used to refute the VSEPR theory that electron-electron repulsion determines geometry. Consider a +8 charge nuclear kernel interacting with four spherical two-electron charge clouds of uniform density and radius R in both square-planar and tetrahedral geometry. The kinetic energy of a uniform single electron charge cloud of radius R is 9/8R2. The intra-pair repulsion is 6/5R and the other electrostatic contributions to the total energy also go like +/- 1/R and are easily determined using elementary geometry. The large spheres in the figures shown below contain two electrons and the small sphere represents the +8 nuclear kernel which is assumed to have the same total energy in both geometries. Further computational detail can be found at http://www.users.csbsju.edu/~frioux/...loudModels.pdf.

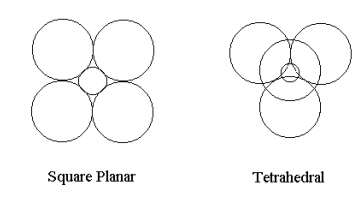
For each geometry the total energy will be minimized with respect to the charge cloud radius using the Mathcad programming environment.

The calculations are carried out in atomic units: h/2π = me = e = a_o = 4πε_o = 1.

Square Planar Geometry

Total energy as a function of R: \( E_D (R) = \frac{9}{R^2} + \frac{8}{R} + \frac{4}{ \sqrt{2} R} + 4 \frac{6}{5R} - \frac{64}{ \sqrt{2}R}\)

Minimize energy with respect to R: \( \begin{matrix} \begin{array}{c|c} R = \frac{d}{dR} E_D (R) = 0 & _{ \text{float, 4}} ^{ \text{solve, R}} \rightarrow 0.6076 \end{array} & E_D (R) = -24.381 \end{matrix}\)

Kinetic energy: \( \frac{9}{R^2} = 24.378\)

Electron-Electron Repulsion: \( \frac{8}{R} + \frac{4}{ \sqrt{2} R} + 4 \frac{6}{5R} = 25.722\)

Electron-nucleus attraction: \( - \frac{64}{ \sqrt{2} R} = -74.481\)

Total potential energy: \( 25.722 - 74.481 = -48.759\)

Average electron-nucleus distance: \( \sqrt{2} R = 0.859\)

Clear R memory: \(R = R\)

Tetrahedral Geometry

Total energy as a function of R: \( E_T (R) = \frac{9}{R^2} + \frac{12}{R} + 4 \frac{6}{5R} - \frac{64}{ \sqrt{ \frac{3}{2}} R}\)

Minimize energy with respect to R: \( \begin{matrix} \begin{array}{c|c} R = \frac{d}{dR} E_T (R) = 0 & _{ \text{float, 4}} ^{ \text{solve, R}} \rightarrow 0.5077 \end{array} & E_T (R) = -34.920 \end{matrix}\)

Kinetic energy: \( \frac{9}{R^2} = 34.916\)

Electron-electron repulsion: \( \frac{12}{R} + 4 \frac{6}{5R} = 33.090\)

Electron-nucleus attraction: \( - \frac{64}{ \sqrt{ \frac{3}{2}} R} = -102.926\)

Total potential energy: \(33.090 - 102.926 = -69.836\)

Average electron-nucleus distance: \( \sqrt{ \frac{3}{2}} R= 0.622\)

These calculations are now summarized in tabular format.

\[ \begin{pmatrix} \text{Energy Contribution} & \text{Square Planar} & \text{Tetrahedral} & \text{Change} \\ \text{Kinetic Energy} & 24.378 & 34.916 & 10.538 \\ \text{Electron electron potential energy} & 25.722 & 33.090 & 7.368 \\ \text{Electron nucleus potential energy} & -74.481 & -102.926 & -28.445 \\ \text{Total energy} & -24.381 & -34.920 & -10.539 \\ \text{Electron nucleus distance} & 0.859 & 0.622 & -0.237 \end{pmatrix} \nonumber \]

Of the three contributions to the total energy, electron-nucleus potential energy has the largest magnitude and is the only negative term. Kinetic energy and electron-electron potential energy have "repulsive" character and are of similar magnitudes for both geometries. They both increase in going from square-planar to tetrahedral geometry, but are overwhelmed by the very large decrease in electron-nuclear potential energy due to the closer proximity of the electrons to the nuclear kernel in the tetrahedral configuration shown in the bottom line of the table. The only conclusion that can be drawn from these calculations is that electron-nuclear attraction determines the configuration of valence electron density around a nonvalence nuclear kernel. And tetrahedral geometry is more stable because it is close-packed and brings the electrons closer to the nucleus than the square planar arrangement.

Further insight can be obtained by graphing the total energy as a function of R for both geometries.

\[ \begin{matrix} R = .2, .21 .. 5 & E_D (R) = \frac{9}{R^2} - \frac{29.626}{R} & E_T (R) = \frac{9}{R^2} - \frac{35.456}{R} \end{matrix} \nonumber \]

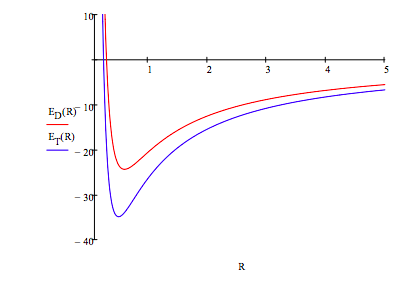
Both the square planar and tetrahedral examples show that it is kinetic energy that is responsibility for the stability of matter. While potential energy is going to negative infinity like -1/R as R decreases, kinetic energy is going to positive infinity like 1/R².