3.23: A Simple Electrostatic Critique of VSEPR

Last updated
Save as PDF

Page ID: 154236

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

In a previous tutorial [1] it was shown that the reason methane is tetrahedral (T_d) rather than square planar (D_4h) is because electron-nucleus attractions are greater for the tetrahedral geometry. VSEPR teaches (incorrectly) that minimization of electron-electron potential energy drives molecular geometry. However, the previous variational calculation showed that electron-electron repulsion is actually higher in T_d methane than it is in the D_4h molecule.

In what follows a simple electrostatic calculation will be presented which reaches the same conclusion as the more elaborate and rigorous variational calculation based on Henry Bent’s [2] Tangent Spheres Model (TSM) of chemical bonding and molecular geometry. This calculation was suggested to the author in a private communication from Henry Bent.

A simple ionic model is proposed for the bonding in methane. The +4 carbon kernel (nucleus and nonvalence electrons) is treated as a point charge which interacts electrostatically with four unpolarized hydride anions of unit diameter in either a square planar or tetrahedral arrangement. In tetrahedral methane the +4 kernel occupies the tetrahedral hole and is not visible in the diagram shown below.

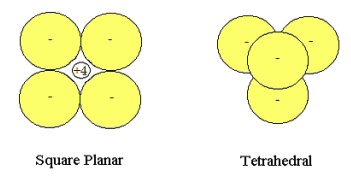
Screen Shot 2019-05-29 at 8.26.42 PM.png

Rudimentary geometrical considerations provide the necessary molecular parameters in the following table.

Molecular Parameter	D_4h	T_d
Hydride-Hydride Distance	4 @ 1 and 2 @ √2	6 @ 1
Hydride-Nucleus Distance	4 @ √2/2	4 @ √(3/8)

From an electrostatic perspective a hydride anion is equivalent to an electron. Therefore, the calculation of the potential energy will be expressed in terms of electron-electron potential energy and electronnucleus potential energy. Using the molecular parameters listed in the table above we calculate the potential energy contributions for both geometries as follows.

Square Planar Methane

\[ \begin{pmatrix} V_{ee} = 4 \frac{(-1)(-1)}{1} + 2 \frac{(-1)(-1)}{ \sqrt{2}} = 5.41 \\ V_{en} = 4 \frac{(-1)(+4)}{ \frac{ \sqrt{2}}{2}} = -22.63 \end{pmatrix} \nonumber \]

Tetrahedral Methane

\[ \begin{matrix} V_{ee} = 6 \frac{(-1)(-1)}{1} = 6.00 \\ V_{en} = 4 \frac{(-1)(+4)}{ \sqrt{ \frac{3}{8}}} = -26.13 \end{matrix} \nonumber \]

These results are summarized in the following table.

Energy Contribution	D_4h	T_d
V_ee	5.41	6.00
V_en	-22.63	-26.13
V_tot	-17.22	-20.13

The results of this simple electrostatic calculation contradict the VSEPR model in two significant ways:

Electron-electron repulsions are greater for tetrahedral geometry than they are for square planar geometry.
T_d is favored over D_4h because of electron-nucleus attractions. In other words, electron-nuclear attractions are the most important energy contribution in determining molecular geometry.

The latter conclusion should not be surprising. There are four types of energy contributions in a molecule under the Born-Oppenheimer approximation: (1) electron kinetic energy; (2) electron-nucleus potential energy; (3) electron-electron potential energy; (4) nucleus-nucleus potential energy. Electronnucleus potential energy is the only attractive term, and electron-electron potential energy is the smallest of the “repulsive” terms. Clearly electron-nucleus attraction is the single most important term in determining molecular geometry.

Furthermore, this guarantees that electron-electron potential energy will track in the opposite direction. Electron domains get closer to nuclei in two ways: by adopting a close-packed geometry (T_d versus D_4h) and by shrinking in size. Both lead to larger electron-electron potential energy and lower (more negative) electron-nucleus potential energy.

For the reasons enumerated above, chemical educators should recall VSEPR. It is not a valid model for molecular geometry and takes up space in textbooks that would be better devoted to viable quantum mechanical models of molecular geometry such as TSM [1, 2] or molecular orbital theory. Even in those textbooks in which it is juxtaposed with more credible models it distracts attention from them because of its specious predictive methodology.

Rioux, F. http://www.users.csbsju.edu/~frioux/vsepr/NVSEPR.htm
Bent, H. A. J. Chem. Educ. 40, 446-452 (1963).