3.14: A One-dimensional Model for the Covalent Bond in the Hydrogen Molecule Ion
- Page ID
- 152894
The covalent bond is a very challenging concept which few chemistry textbooks treat adequately. The simplest example of a covalent bond is the one‐electron bond in the hydrogen molecule ion. It plays the same role in the study of chemical bonding that the hydrogen atom plays in the study of atomic structure. The most penetrating, extensive, and perhaps controversial, analysis of the H2+ bond was provided by Ruedenberg over forty years ago (Rev. Mod. Phys. 1962, 34, 326‐352). The goal of this tutorial is quite modest in comparison; here an attempt is made to capture several of the basic features of the covalent bond with a simple, and yet plausible, one‐dimensional model.
This tutorial uses a one‐dimensional, double‐well potential (double Posch‐Teller potential) to model the H2+ covalent bond. Schrödingerʹs equation is solved numerically for the two lowest energy states using Mathcadʹs ordinary differential equation solver, and the numerical results are displayed graphically and interpreted. The calculations are carried out in atomic units: e = me = h/2π = 1.
As a numerical model, this approach is not based on the molecular orbital method (LCAO ‐ linear combination of atomic orbitals), but as we will see its results are consistent with the LCAO‐MO model for chemical bonding.
ODE Numerical Integration Algorithm
The Posch‐Teller parameters were determined by adjusting V0 so that it gave the correct H2+ ground state energy (‐0.6029 Eh) at the equilibrium bond length (2.00 a0).
\[ \begin{matrix} \text{Parameters:} & m = 1 & x_{max} = 8 & V_o = -1.11223 & \alpha = 1.5 & d = 1 \end{matrix} \nonumber \]
\[ \begin{matrix} \text{Potential energy:} & V(x) = V_o \left[ \frac{1}{ \cosh [ \alpha (x-d)]^2} + \frac{1}{ \cosh [ \alpha (x+d)]^2} \right] \end{matrix} \nonumber \]
Solve Schrödingerʹs equation numerically, and normalize and display the solution:
\[ \begin{matrix} \text{Given} & \frac{-1}{2m} \frac{d^2}{dx^2} \Psi (x) + V(x) \Psi (x) = E \Psi (x) & \Psi \left( - x_{max} \right) = 0 & \Psi ' \left( - x_{max} \right) = 0.1 \end{matrix} \\ & \Psi = \text{Odesolve} \left( x,~x_{max} \right) &
N = \frac{1}{ \sqrt{ \int_{-x_{max}}^{x_{max}} \Psi (x)^2 dx}} & \Psi (x) = N \Psi(x) \end{matrix} \nonumber \]
Enter energy: E = =0.6029
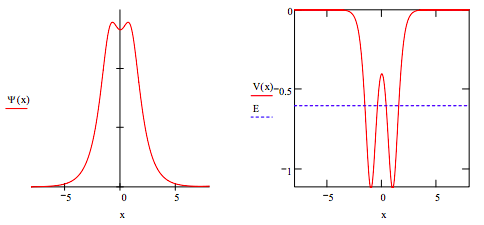
This result for the ground state correctly shows that the electron density is delocalized over both nuclear centers forming a molecular state. It also shows that the electron density is greatest at the nuclear centers where the electron‐nucleus potential energy is lowest, and dips somewhat in the ʺbond regionʺ where the potential energy is much higher. It also shows that tunneling is occurring because the electron is present in regions where its total energy is lower than the local potential energy. Inspection of the right‐hand figure above shows that tunneling occurs for the following situations: x < ‐1.55, x > 1.55, and ‐0.396 < x < 0.396. The probability that tunneling is occuring is calculated below.
\[ \int_{-1.56}^{x_{max}} \Psi (x)^2 dx + \int_{-0.396}^{0.396} \Psi (x)^2 dx + \int_{1.56}^{x_{max}} \Psi (x)^2 dx = 0.229 \nonumber \]
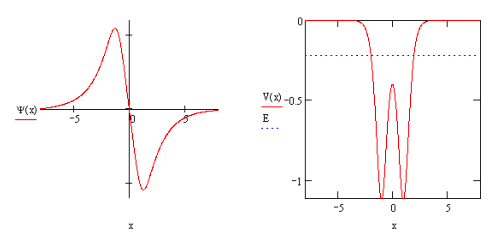
The next allowed state with energy E = ‐0.2222 Eh is clearly anti‐bonding because of the node in the internuclear region. The model also shows that this anti‐bonding state is unstable relative to a hydrogen atom and hydrogen ion which collectively have an energy of ‐0.500 Eh.