3.11: A Mechanistic Approach to Bond Formation in the Hydrogen Molecule Ion

The centrality of the covalent bond to chemistry is captured in a short and eloquent statement by Peter Atkins [1].

Now we come to the heart of chemistry. If we can understand what holds atoms together as molecules we may also start to understand why, under certain conditions, old arrangements change in favor of new ones. We shall understand structure, and through structure, the mechanism of change.

The barrier to understanding is that, in spite of what our textbooks teach, ʺThe chemical bond is a highly complex phenomenon which eludes all attempts at simple description [2].ʺ Charles Coulson, one of the pioneering theorists in the application of quantum mechanics to the study of chemical bonding wrote the following [3].

Sometimes it seems to me that a bond between two atoms has become so real, so tangible, so friendly that I can almost see it. And then I awake with a little shock: for a chemical bond is not a real thing: it does not exist: no one has ever seen it, no one ever can. It is a figment of our own imagination.... Here is a strange situation. The tangible, the real, the solid, is explained by the intangible, the unreal, the purely mental.

Many chemists and physicists have grappled with the intellectual challenge of understanding the chemical bond. Among those who have made significant contributions are Hellmann [4], Pauling [5], Slater [6, 7], Coulson [8] and Ruedenberg [9-12]. Among these, Ruedenbergʹs work is the most comprehensive and cogent. It has received considerable attention in the pedagogical literature [13‐23] as well as a number of excellent reviews in the primary literature that are accessible to non specialists [24-26].

Unfortunately none of these efforts to make Ruedenbergʹs analysis of the covalent bond accessible to educators has had any noticeable affect on the way the chemical bond is presented in introductory and intermediate level undergraduate textbooks [27]. Therefore, the purpose of this paper is to try again by providing a simple two-step mechanistic approach to covalent bond formation in H₂⁺ that reveals Ruedenbergʹs central message - a full understanding of the nature of the chemical bond requires consideration of the role of electron kinetic energy, or more appropriately confinement energy [28].

The mechanism postulates a single intermediate molecular state for the H₂⁺ bond formation reaction.

\[ H + H^+ \rightarrow H_2^+ \nonumber \]

Scaled hydrogenic wave functions will be used to calculate the initial atomic state, and the intermediate and final molecular states. Computational details for the intermediate and final molecular states are available in the appendix.

The Initial State

Schrödingerʹs equation for the hydrogen atom, of course, is exactly soluble and the result in atomic units (h/2π = m_e = e = 4πε₀ = 1; E_h = 4.3597x10^-18 J) is given below. By convention the energy of the hydrogen ion is zero.

\[ E_H = T + V = 0.50E_h - 1.0E_h = -0.50E_h \nonumber \]

The Hydrogen Molecule Ion

The H₂⁺ molecular orbital is written as a linear superposition of scaled hydrogenic orbitals centered on the two hydrogen nuclei, where S is the overlap integral. (a and b label the atomic orbitals, A and B the nuclear centers which are separated by a distance R.

\[ \Psi_{mo} = \frac{a+b}{ \sqrt{2 + 2S}} \nonumber \]

where

\[ \begin{matrix} a = \sqrt{ \frac{ \alpha^3}{ \pi}} \text{exp} ( - \alpha r_A ) & b = \sqrt{ \frac{ \alpha^3}{ \pi}} \text{exp} ( - \alpha r_B ) & S = \int ab d \tau \end{matrix} \nonumber \]

This trial wave function and the appropriate energy operator lead to the following variational energy integral, expressed in Dirac notation.

\[ E = \left( a + b \left| T - \frac{1}{r_A} - \frac{1}{r_B} + \frac{1}{R} \right| a + b \right) [2 (1+S)]^{-1} \nonumber \]

Expansion, after symmetry considerations, yields the following expression,

\[ E = \frac{(a |T| a) + (a|T| b) + \left( a \left| \frac{-1}{r_A} \right| a \right) + \left( b \left| \frac{-1}{r_A} \right| b \right) +2 \left( a \left| \frac{-1}{r_A} \right| b \right)}{1+S} + \frac{1}{R} \nonumber \]

which is written below in short-hand notation.

\[ E = \frac{T_{aa} + T_{ab} + V_{Aaa} + V_{Abb} + 2V_{Vab}}{1+S} + \frac{1}{R} \nonumber \]

Minimization of the energy of H₂⁺ yields the optimum values for α and R, its ground state energy and energy components. Table 1 summarizes the results for the formation of the molecule ion from a hydrogen atom and hydrogen ion.

\[ \begin{pmatrix} o & \frac{ \text{Initial}}{ \text{Atomic State}} & o & \frac{ \text{Final}}{ \text{Molecular State}} \\ o & H_{atom} + H_{ion} & o & \Psi_{mo} = \frac{a+b}{ \sqrt{2 + 2S}} \\ o & \alpha = 1 & \Delta & \frac{ \alpha = 1.238}{R = 2.003} \\ T & 0.5 & 0.0865 & 0.5865 \\ V & -1.0 & -0.1730 & -1.1730 \\ V_{ne} & -1.0 & -0.6723 & -1.6723 \\ V_{ne} (Aaa) & -1.0 & 0.1539 & -0.8461 \\ V_{ne} (Abb) & 0 & -0.3329 & -0.3329 \\ V_{ne} (Aab) & 0 & -0.4933 & -0.4933 \\ V_{nn} & 0 & 0.4993 & 0.4993 \\ E & -0.5 & -0.0865 & -0.5865 \end{pmatrix} \nonumber \]

V_ne(Aaa) is the interaction of the electron density centered on nucleus A with nucleus A. V_ne(Abb) is the interaction of the electron density centered on nucleus B with nucleus A. V_ne(Aab) is the interaction of the overlap electron density with nucleus A. These energy contributions include the companion terms involving nucleus B as justified by molecular symmetry.

Table 1 shows that the atomic and molecular states individually satisfy the virial theorem (E = V/2 = -T), and therefore so does the bond formation process (ΔE = ΔV/2 = -ΔT). At first glance Table 1 and the virial theorem suggest that chemical bonding is governed solely by electrostatics. In bond formation, in the transition from atoms to a molecule, kinetic energy increases, potential energy decreases, and total energy decreases. From this perspective it appears that potential energy must be the key factor in the formation of a stable molecule, because it has the same sign as the change in total energy, and a decrease in energy is the signature of stability. That this view is an over-simplification is shown by the energy profile (in atomic units) provided by an ab initio calculation of covalent bond formation in the hydrogen molecule ion using the trial molecular orbital given above.

Figure 1. Ab initio energy profile for the formation the hydrogen molecule ion.

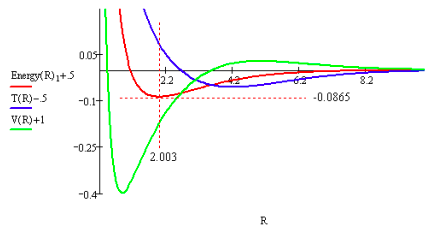
This energy profile shows that consideration of kinetic energy is essential in understanding bond formation and molecular stability. First, the initial drop in total energy as the nuclei approach each other is due to a decrease in kinetic energy, because the potential energy initially increases. Second, the energy minimum (ground state) is achieved while potential energy is in a steep decline. It is a sharp increase in kinetic energy that causes the energy minimum and provides the ʺrepulsiveʺ effect necessary to counter the (still) attractive potential energy term. As the profile shows nuclear repulsion doesnʹt become dominant until well after the energy minimum has been reached. Clearly a valid model for the covalent bond requires consideration of both kinetic and potential energy.

These ab initio results are supported by a more empirical approach based on the virial theorem, a method of analysis first demonstrated by Slater in 1933 [5]. A serviceable representation of molecular energy for diatomic molecules (excluding nuclear kinetic energy, i.e. vibrational degrees of freedom) is provided by the Morse function.

\[ E(R) = D_e \left[ 1 - \text{exp} \left[ - \beta \left( R - R_e \right) \right] \right]^2 - D_e \nonumber \]

The Morse parameters (De, Re and β) can be obtained from analysis of spectroscopic data. Therefore, using the Morse function with the general expression for the virial theorem (valid for both the classical and quantum mechanical domains)

\[ 2T(R) + V(R) = - R \frac{d}{dR} E(R) \nonumber \]

and the expression for total energy

\[ E(R) = T(R) + V(R) \nonumber \]

leads to the following equations for kinetic and potential energy as a function of internuclear separation.

\[ \begin{matrix} T(R) = -E(R) - R \frac{d}{dR} E(R) & V(R) = 2E(R) + R \frac{d}{dR} E(R) \end{matrix} \nonumber \]

Using spectroscopic parameters from the literature [29] for H₂⁺ allows the generation of the following energy profile in atomic units.

Figure 2. Energy profile for the formation of the hydrogen molecule ion based on the virial theorem.

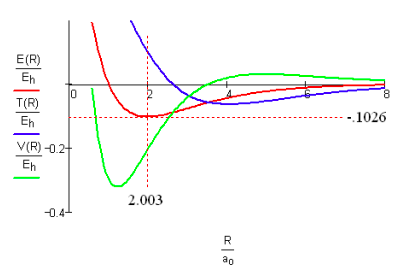
The basic agreement between Figure 1 (theoretical, ab initio) and Figure 2 (experimental, spectroscopic) supports the view that both kinetic and potential energy considerations are required for a viable model of the covalent bond; models that consider only electrostatic potential energy effects are invalid and misleading.

In Figures 1 and 2 the fact that the potential energy increases, then decreases, and finally increases again as R decreases suggests that it can be partitioned into three terms. The initial decrease in kinetic energy is followed by an increase indicating that it consists of two opposing contributions. Thus, Ruedenberg analyzed the H₂⁺ bond formation in terms of five contributions to the binding energy. In an effort to make Ruedenbergʹs ideas accessible to undergraduates, a simple two-step mechanistic approach will be used to interpret covalent bond formation.

As shown below, the mechanism postulates an intermediate molecular state at the equilibrium bond length, but with the atomic value for the orbital scale factor, α. Computational details on the intermediate state are provided in the appendix.

\[ H ( \alpha = 1) + H^+ \rightarrow H_2^+ ( \alpha = 1,~R = 2.003) \rightarrow H_2^+ ( \alpha = 1.238,~R = 2.003) \nonumber \]

\[ \begin{pmatrix} o & \frac{ \text{Initial}}{ \text{Atomic State}} & o & \frac{ \text{Intermediate}}{ \text{Molecular State}} & o & \frac{ \text{Final}}{ \text{Molecular State}} \\ o & H_{atom} + H_{ion} & o & \Psi_{imo} = \frac{a+b}{ \sqrt{2+2S}} & o & \Psi_{mo} = \frac{a+b}{ \sqrt{2+2S}} \\ o & \alpha = 1 & \Delta & \frac{ \alpha = 1}{R=2.003} & \Delta & \frac{ \alpha=1.238}{R=2.003} \\ T & 0.5 & -0.1138 & 0.3862 & 0.2003 & 0.5865 \\ V & -1.0 & 0.0599 & -0.9401 & -0.2329 & -1.1730 \\ V_{ne} & -1.0 & -0.4394 & -1.4394 & -0.2329 & -1.6723 \\ V_{ne}(Aaa) & -1.0 & 0.3693 7 -0.6307 & -0.2154 & -0.8461 \\ V_{ne}(Abb) & 0 & -0.2976 & -0.2976 & -0.0353 & -0.3329 \\ V_{ne}(Aab) 0 & -0.511 & -0.511 & 0.0178 & -0.4933 \\ V_{nn} 0 & 0.4993 & 0.4993 & 0 & 0.4993 \\ E & -0.5 & -0.0539 & -0.5539 & -0.0326 & -0.5865 \end{pmatrix} \nonumber \]

The first step is exoergic and is driven by a decrease in electron kinetic energy. Charge delocalization over the two nuclear centers on the formation of the molecular orbital brings about a large decrease in kinetic energy (-0.1138 E_h) because of the larger molecular volume now available to the electron [28]. Potential energy increases (+0.0599 E_h) because nuclear repulsion (+0.4993 E_h) is larger than the decrease electron-nucleus potential energy (-0.4394 E_h), which consists of the three contributions shown in Table 2. Constructive interference between atomic orbitals during molecular orbital formation draws some electron density into the internuclear region where potential energy is higher than in the region around the nucleus. Thus, the significant increase in Vne(Aaa) (+0.3693 E_h) is the main reason that the decrease in the attractive V_ne term is less than the increase in the repulsive V_nn term.

The second step is also exoergic, but is driven by a decrease in potential energy. In this step the atomic orbitals making up the molecular orbital contract (α increases from 1 to 1.238) to achieve the final equilibrium molecular state. Orbital contraction draws electron density from the bond region back toward the nuclei - it returns some of the charge density transferred to the bond region in the first step back to the nuclear centers. This is evidenced by the significant decrease in V_ne(Aaa) (-0.2154 E_h) and the change in the overlap integral from 0.5856 for α = 1 to 0.4632 for α = 1.238 (see the appendix). The changes in V_ne(Abb) and V_ne(Aab) are relatively minor in this step. Potential energy decreases (-0.2329 E_h) because the electron is on average closer to the nuclei. Kinetic energy increases (+0.2003 E_h) because orbital contraction decreases the volume occupied by the electron [28].

This mechanism is consistent with the computational results summarized in Figures 1 and 2, and therefore, reiterates that a consideration of both kinetic and potential energy effects are required to understand the nature of the covalent bond. Electron-nucleus potential energy is the only negative (attractive) energy term and is the ʺglueʺ that holds the molecule together. Paradoxically kinetic energy plays two contradictory roles in covalent bond formation. Its initial decrease due to charge delocalization funds the build up of charge in the internuclear region and is responsible for the early drop in total energy, while its subsequent sharp increase due to orbital contraction insures a ground state and a stable molecular entity.

To summarize further we can say that the first step is molecular in character and is driven by a decrease in electron kinetic energy. The second step, orbital contraction, is atomic in character (drawing electron density back to the nuclei) and driven by a decrease in electron-nucleus potential energy.

Literature cited:

1. Atkins, P. W. Molecular Quantum Mechanics, 2nd ed.; Oxford University Press, Oxford, UK, 1983, p.250.
2. Kutzelnigg, W. Angew. Chem. internat. Edit. 1973, 12, 546-562.
3. Coulson, C. A. J. Chem. Soc. 1955, 2069.
4. Hellmann, H. Z. Phys. 1933, 35, 180.
5. Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press, Ithaca, NY, 1960.
6. Slater, J. C. J. Chem. Phys. 1933, 1, 687-691.
7. Slater, J. C. Quantum Theory of Matter, Krieger Publishing: Untington, NY, 1977; pp 405-408.
8. Coulson, C. A. Valence, 2nd ed.; Oxford University Press, Oxford, UK, 1961.
9. Ruedenberg, K. Rev. Mod. Phys. 1962, 34, 326-352.
10. Feinberg, M. J.; Ruedenberg, K. J. Chem. Phys. 1971, 54, 1495-1511. Feinberg, M. J.; Ruedenberg, K. J. Chem. Phys. 1971, 55, 5804-5818.
11. Ruedenberg, K. In Localization and Delocalization in Quantum Chemistry; Chalvet, O. et al., Eds.; Reidel: Dordrecht, The Netherlands, 1975; Vol. I, pp 223-245.
12. Ruedenberg, K.; Schmidt, M. W. J. Comput. Chem. 2007, 28, 391-410. Ruedenberg, K.; Schmidt, M. W. J. Phys. Chem. A 2009, 113, 1954-1968.
13. Harcourt, R. D.; Solomon, H.; Beckworth. J. Am. J. Phys. 1982, 50, 557-559.
14. Baird, N. C. J. Chem. Educ. 1986, 63, 660-664.
15. Harcourt, R. D. Am. J. Phys. 1988, 56, 660-661.
16. Nordholm, S. J. Chem. Educ. 1988, 65, 581-584.
17. Bacskay, G. G.; Reimers, J. R.; Nordholm, S. J. Chem. Educ. 1997, 74, 1494-1502.
18. Weinhold, F. J. Chem. Educ. 1999, 76(8), 1141-1145.
19. Rioux, F. Chem. Educator 1997, 2(6), 1-14.
20. Rioux, F. Chem. Educator 2001, 6(5), 288-290.
21. Rioux, F. Chem. Educator 2003, 8(1), 10-12.
22. Ashkenazi, G; Kosloff, R. Chem. Educator 2006, 11(2), 67-76.
23. Nordholm, S.; Back, A.; Bacskay, G. B. J. Chem. Educ. 2007, 84, 1201-1203.
24. Kutzelnigg, W. Angew. Chem. Int. Ed. Eng. 1973, 12, 546-562.
25. Melrose, M. P.; Chauhan, M.; Kahn, F. Theor. Chim. Acta 1994, 88, 311-324.
26. Gordon, M. S.; Jensen, J. H. Theor. Chem. Acc. 2000, 103, 248-251.
27. An exception is the physical chemistry text by Jeff Davis which provides a concise and coherent quantum mechanically correct interpretation of the covalent bond. Unfortunately it is long out of print. Davis, J. C., Advanced Physical Chemistry: Molecules, Structure, and Spectra; The Ronald Press, New York, 1965; pp 427-428.
28. Electrons confined by attractive interaction with nuclei in atoms and molecules occupy, due to their wave nature, stationary states. They are not executing classical trajectories and consequently the term kinetic energy is inappropriate. Substitution of the de Broglie relation (p = h/λ) into the classical expression for kinetic energy yields the electronʹs confinement energy, h²/2mλ². Because the wavelength of a confined electron is proportional to the confinement dimension, it is also proportional to cube root of the confinement volume, V1/3. Therefore the electronʹs confinement energy is proportional to V^-2/3.
29. Levine, I. N. Quantum Chemistry, 6^th ed., Pearson Prentice Hall, Upper Saddle River, NJ, 2009; p 400.

Appendix

\( \colorbox{yellow}{Overlap integral:}\)

\[ S( \alpha,~R) = \text{exp}( - \alpha,~R) \left( 1 + \alpha R + \frac{ \alpha^2 R^2}{3} \right) \nonumber \]

\( \colorbox{yellow}{Kinetic energy integrals:}\)

\[ \begin{matrix} Taa ( \alpha,~R) = \frac{ \frac{1}{2} \alpha^2}{1 + S( \alpha,~R)} & Tab( \alpha,~R) = \frac{ \frac{ \alpha^2}{2} \text{exp} ( - \alpha R) \left( 1 + \alpha R - \frac{ \alpha^2 R^2}{3} \right)}{1 + S ( \alpha,~R)} \end{matrix} \nonumber \]

\( \begin{matrix} \colorbox{yellow}{Potential energy integrals:} & VAaa ( \alpha,~R) = \frac{ - \alpha}{1 + S( \alpha,~R)} \end{matrix}\)

\[ \begin{matrix} VAbb( \alpha,~R) = \frac{ - \alpha \left[ \frac{1}{ \alpha R} - \text{exp} (-2 \alpha R) \left( 1 + \frac{1}{ \alpha R} \right) \right]}{1 + S( \alpha,~R)} & VAab ( \alpha,~R) = \frac{- \alpha \text{exp} ( - \alpha R) (1 + \alpha R)}{1 + S( \alpha,~R)} \end{matrix} \nonumber \]

\( \colorbox{yellow}{Intermediate Molecular State}\)

\[ \begin{matrix} \colorbox{yellow}{Values of variational parameters:} & \alpha = 1 & R = 2.003 & \colorbox{yellow}{Overlap integral:} & S( \alpha,~R) = 0.5856 \end{matrix} \nonumber \]

\[ \begin{matrix} \colorbox{yellow}{Total energy:} & Taa ( \alpha,~R) + Tab ( \alpha,~R) + VAaa ( \alpha,~R) + VAbb ( \alpha,~R) + 2 VAab ( \alpha,~R) + \frac{1}{R} = -0.5539 \end{matrix} \nonumber \]

\[ \begin{matrix} \colorbox{yellow}{Kinetic energy:} & Taa ( \alpha,~R) + Tab ( \alpha,~R) = 0.3862 & Taa ( \alpha,~R) = 0.3153 & Tab ( \alpha,~R) = 0.0709 \end{matrix} \nonumber \]

\[ \begin{matrix} \colorbox{yellow}{Electron-nucleus potential energy:} & VAaa ( \alpha,~R) + VAbb ( \alpha,~R) + 2 VAab ( \alpha,~R) = -1.4394 \end{matrix} \nonumber \]

\[ \begin{matrix} VAaa ( \alpha,~R) = =0.6307 & VAbb ( \alpha,~R) = -0.2976 & 2VAab ( \alpha,~R) = -0.5111 \end{matrix} \nonumber \]

\[ \begin{matrix} \colorbox{yellow}{Nuclear potential energy:} & \frac{1}{R} = 0.4993 \\ \colorbox{yellow}{Total potential energy:} & VAaa ( \alpha,~R) + VAbb ( \alpha,~R) + 2VAab ( \alpha,~R) + \frac{1}{R} = -0.9401 \end{matrix} \nonumber \]

\( \colorbox{yellow}{Final Molecular State}\)

\[ \begin{matrix} \colorbox{yellow}{Values of variational parameters:} & \alpha = 1.238 & R = 2.003 & \colorbox{yellow}{Overlap integral:} & S ( \alpha,~R) = 0.4632 \end{matrix} \nonumber \]

\[ \begin{matrix} \colorbox{yellow}{Total Energy:} & Taa ( \alpha,~R) + Tab ( \alpha,~R) + VAaa ( \alpha,~R) + VAbb ( \alpha,~R) + 2VAab ( \alpha,~R) + \frac{1}{R} = -0.5865 \end{matrix} \nonumber \]

\[ \begin{matrix} \colorbox{yellow}{Kinetic energy:} & Taa ( \alpha,~R) + Tab ( \alpha,~R) = 0.5865 & Taa ( \alpha,~R) = 0.5237 & Tab ( \alpha,~R) = 0.0627 \end{matrix} \nonumber \]

\[ \begin{matrix} \colorbox{yellow}{Electron-nucleus potential energy:} & Vaa ( \alpha,~R) + VAbb ( \alpha,~R) + 2 VAab ( \alpha,~R) = -1.6722 \end{matrix} \nonumber \]

\[ \begin{matrix} VAaa ( \alpha,~R) = -0.8461 & VAbb ( \alpha,~R) = -0.3329 & 2VAab ( \alpha,~R) = -0.4933 \end{matrix} \nonumber \]

\[ \begin{matrix} \colorbox{yellow}{Nuclear potential energy:} & \frac{1}{R} = 0.4993 \\ \colorbox{yellow}{Total potential energy:} & VAaa ( \alpha,~R) + VAbb ( \alpha,~R) + 2VAab ( \alpha,~R) + \frac{1}{R} = -1.1730 \end{matrix} \nonumber \]