3.4: Brief Version of the Covalent Bond Clarified Through the Use of the Virial Theorem

Abstract: The chemical bond is a concept of unique importance in chemistry that students first study seriously in a college or university general chemistry course. At first glance, the descriptions of covalent bond formation found in general chemistry texts seem plausible and comprehensible; however, when they are examined more carefully, it is found that they violate both classical and quantum mechanical principles.

Introduction

In the second edition of his classic text, Molecular Quantum Mechanics, Peter Atkins begins the chapter on molecular structure with the following sentences [1]:

Now we come to the heart of chemistry. If we can understand what holds atoms together as molecules we may also start to understand why, under certain conditions, old arrangements change in favor of new ones. We shall understand structure, and through structure, the mechanism of change.

Few will argue with Atkins' eloquent assertion that the chemical bond is at the heart of chemistry, but where do we find an accurate explanation of chemistry's central concept?-certainly not in chemistry textbooks written for undergraduate audiences. For example, a survey of widely adopted general chemistry texts showed the following errors in the description of the covalent bond to be prevalent.

• The covalent bond is presented as a purely electrostatic phenomenon. Electron kinetic energy is never mentioned, even though the total energy of a molecule is a sum of kinetic and potential energy contributions, and atomic and molecular stability cannot be understood solely in terms of potential energy.
• Closely related to this is what is actually an energy curve is called a potential energy curve. What is shown in introductory texts is the total molecular energy as a function of internuclear separation under the Born-Oppenheimer approximation. In other words, nuclear kinetic energy is frozen, but electron kinetic energy contributes to the total molecular energy.
• It is claimed that the electron density in the internuclear (bond) region has a lower potential energy because it is attracted to two nuclei. Actually using simple electrostatic arguments (see the appendix) it is easy to show that the electron-nuclear potential energy is higher in the internuclear region than it is closer to either of the nuclei. On the basis of potential energy alone the electrons would prefer to be in the nucleus.
• It is claimed that an energy minimum, or molecular ground state, is achieved because of increases in nuclear- nuclear and electron-electron repulsions as the internuclear separation decreases. As will be shown later, the immediate cause of the molecular ground state is a sharp increase in electron kinetic energy.
• The amount of electron density transferred to the bonding region is greatly overstated, sometimes implying that a pair of electrons is shared in the space between two nuclei rather than by two nuclei.

By comparison, these errors are not often found in physical chemistry textbooks. Most physical chemistry texts set up the Schrödinger equation for the H₂⁺ and H₂ molecules and outline the solutions, but avoid interpreting the calculations other than saying something to the effect that the chemical bond is a quantum mechanical phenomenon that has no classical analog or explanation. A notable exception is the text by Atkins and de Paula, which gives a correct analysis of the bond in H₂⁺ in a footnote and the text by Raff, which summarizes the best ab initio results for H₂ [2]. Thus, in order to find an accurate analysis of covalent bond formation, it is necessary to consult advanced quantum chemistry texts, the research literature, or the pedagogical literature.

In the 1960s and 70s Ruedenberg and his collaborators carried out a detailed quantum mechanical study of the covalent bond in H2 + [3-5]. The most important conclusion of this thorough and insightful study was that electron kinetic energy plays a crucial role in chemical bond formation. Ruedenberg's contributions to the understanding of the chemical bond have been summarized in the pedagogical literature [6-11] and in review articles [12-14]. It is unfortunate that none of these efforts to make Ruedenberg's work accessible to the nonspecialist have had any noticeable impact on the way chemical bonding is presented by authors of chemistry textbooks at the introductory or intermediate level.

It is not widely appreciated that John Slater came to similar conclusions about covalent bond formation thirty years before Ruedenberg using a more empirical approach based directly on the virial theorem [15-17]; therefore, the purpose of this paper is to outline Slater's method for the hydrogen molecule, the simplest example of the traditional two-electron chemical bond. It should be noted, however, that Slaterís approach is appropriate for any diatomic molecule for which Morse parameters are available.

Figure 1. Energy profile for H₂ using the virial theorem and a Morse function with spectroscopic parameterization.

Background Theory

In the early days of the quantum revolution Slater used the virial theorem to analyze the chemical bond and was the first to notice the importance that electron kinetic energy played incovalent bond formation. With regard to the virial theorem he said [15]:

...this theorem gives a means of finding kinetic and potential energy separately for all configurations of the nuclei, as soon as the total energy is known, from experiment or theory.

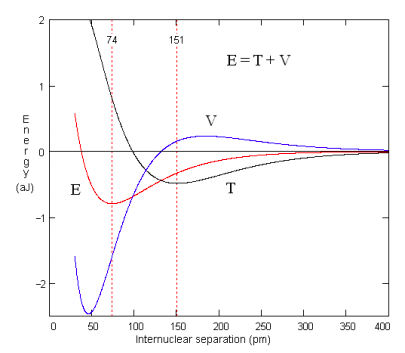
Under the Born-Oppenheimer approximation, the molecular energy as a function of internuclear separation, E(R), is represented well by a Morse function [18] whose parameters for H2 are based on spectroscopic data: De = 7.93 aJ; β = 0.0190 pm^-1; Re = 74.1 pm [19].

\[ E(R) = D_e \left[ 1 - \text{exp} \left( - \beta (R- R_e ) \right) \right]^2 - D_e \nonumber \]

The virial theorem for diatomic molecules [15] can be used with eq 1 to obtain expressions for the average values of kinetic and potential energy as a functions of the internuclear separation, R.

\[ T(R) = - E(R) - R \frac{dE(R)}{dR} \nonumber \]

\[ V(R) = 2E(R) + R \frac{dE(R)}{dR} \nonumber \]

Quoting Slater again [15]:

These important equations determine the mean kinetic and potential energies as functions of R, one might almost say, experimentally, directly from the curves of E as a function of R which can be found from band spectra. The theory is so simple and direct that one can accept the results without question...

When eq 1, parameterized as indicated earlier, is used in eqs 2 and 3, the energy profile for covalent bond formation in H2 shown in the Figure 1 is obtained.

Analysis

As Slater pointed out, the molecular energy curve can be obtained from experiment (spectroscopy) or theory (ab initio quantum mechanics). The energy profile obtained is similar in both approaches. For example, Winn [20] offered the following analysis of the ab initio results of Kolos and Wolniewicz [21] for H₂.

As the atoms approach, the potential energy rises (electrons are moving away from nuclei) and the kinetic energy falls (as delocalization begins). In the vicinity of R/R_e = 2, this trend reverses. The kinetic energy increases as the electronic wave function is localized further, raising the momentum, but the potential energy falls, as charge is now brought nearer both nuclei. Only at R/R_e < 0.5 does nuclear repulsion cause the potential energy to increase and contribute to the total repulsion energy.

This analysis will serve as the basis for a simple quantum mechanical model for covalent bond formation consistent with the spectroscopic energy profile shown in Figure 1 that uses qualitative concepts accessible to introductory students. It consists of two steps: (1) molecular orbital formation through the overlap of atomic orbitals, followed by (2) atomic orbital contraction. It is assumed step (1) ends as kinetic energy reaches a minimum (151 pm), and step (2) ends when the total energy reaches a minimum (74.1 pm). This approach yields the following quantitative analysis of bond formation in H₂.

	Step 1	Step 2	Overall
ΔT/aJ	-0.495	1.288	0.793
ΔV/aJ	0.159	-1.745	-1.586
ΔE/aJ	-0.336	-0.457	-0.793
R/pm	151	74.1	74.1

1. The constructive interference that accompanies molecular orbital formation brings about charge delocalization and charge redistribution. This step is molecular in character and is driven by a decrease in kinetic energy as the table above shows.

Charge delocalization occurs because each electron now belongs to both nuclei and occupies a larger volume than in the atomic state. This effect is accompanied by a significant decrease in electron kinetic energy [22]. Charge redistribution occurs because atomic overlap transfers some electron density away from the nuclear centers into the internuclear (overlap) region, which involves an increase in potential energy. Overall this step is exothermic because kinetic energy decreases more than potential energy increases. Thus, charge delocalization funds the redistribution of charge into the internuclear region that is normally associated with bond formation.

2. The reduction of electron density near the nuclei that occurs in step 1 allows the atomic orbitals to contract returning some electron density to the nuclear centers from the internuclear region. This step is atomic in character and is driven by a large decrease in potential energy.

The decrease in potential energy occurs because the electrons are brought closer to the nuclei, and the increase in kinetic energy occurs because orbital contraction has reduced the volume occupied by the electrons, thereby reducing the level of delocalization. It has been shown that at the equilibrium bond distance the net transfer of electron density into the internuclear region is only 16% [5].

According to the energy profile, an energy minimum is reached while the potential energy is still in a significant decline, showing that kinetic energy, which is increasing rapidly, is the immediate cause of a stable bond and molecular ground state in H₂. The final increase in potential energy, which is mainly due to nuclear-nuclear repulsion, doesn't begin until the internuclear separation is less than 50 pm and the equilibrium bond length is 74 pm. Thus, the common explanation that an energy minimum is reached because of nuclear-nuclear and electron-electron repulsion does not have merit. As Ruedenberg [5] has succinctly noted "there are no ground states in classical mechanics or electrostatics".

Conclusion

In summary, an "empirical" analysis of the covalent bond in H₂ has been presented based on the virial theorem and a Morse molecular energy function parameterized using spectroscopic data. This analysis shows that the role of electron kinetic energy in covalent bond formation runs counter to conventional wisdom in two seemingly paradoxical ways. First, a decrease in kinetic energy due to incipient molecular orbital formation funds the transfer of charge density into the internuclear region, lowering the total energy. Second, a large increase in kinetic energy accompanying the subsequent atomic orbital contraction prevents the collapse of the molecule, and causes an energy minimum and a stable molecular ground state.

Clearly, using rigorous quantum mechanics in introductory chemistry courses in order to avoid error in describing the chemical bond is not a practical solution; however, teaching simple, easily digestible, but incorrect models for the covalent bond is pedagogically unacceptable. It is therefore necessary to offer general chemistry students an explanation of the nature of the covalent bond that is both correct and accessible. To achieve this end a rudimentary two-step quantum mechanical mechanism for covalent bond formation in H₂ has been proposed.

Appendix

When asked what motivated the creation of his famous model of the atom Bohr replied "the stability of matter, a pure miracle when considered from the standpoint of classical physics." The following simple calculation will demonstrate what Bohr meant by this statement. This calculation will be carried out in atomic units where the charge on the electron is ñ1, the charge on the nucleus +1, and distances are measured in bohr, a_o.

Two nuclei (Z = 1) are placed at x = 0.0 and 2.0, respectively. An electron is located exactly between them at x = 1.0, where we instinctively, but incorrectly, think it would want to be on the basis of electrostatic considerations. The potential energy consists of three interactions (nuclear-nuclear repulsion and two electron-nuclear attractions) and is calculated as follows:

\[ V = \frac{(+1)(+1)}{2} + \frac{(-1)(+1)}{2} + \frac{(-1)(+1)}{1} = -1.50 \nonumber \]

Now move the electron 0.5 a_o closer to one of the nuclei.

\[ V = \frac{(+1)(-1)}{2} + \frac{(-1)(+1)}{0.5} + \frac{(-1)(+1)}{1.5} = -2.17 \nonumber \]

And so it goes, on the basis of electrostatic considerations, until the electron is inside one nucleus or the other. Although the electron was treated as a point charge in this calculation, a rigorous quantum mechanical calculation tells the same story-moving charge to the internuclear region increases electrostatic potential energy.

References and Notes

1. Atkins, P. W. Molecular Quantum Mechanics; Oxford University Press, Oxford, UK, 1983, p. 250.
2. (a) Atkins, P.; de Paula, J. Physical Chemistry, 7^th ed.; W. H. Freeman and Co.: New York, 2002; p 420; (b) Raff, L. M. Principles of Physical Chemistry; Prentice Hall: Upper Saddle River, NJ, 2000; pp 761-764.
3. Ruedenberg, K. Rev. Mod. Phys. 1962, 34, 326-352.
4. Feinberg, M. J.; Ruedenberg, K. J. Chem. Phys. 1971, 54, 1495-1511; Feinberg, M. J.; Ruedenberg, K. J. Chem. Phys. 1971, 55, 5804-5818.
5. Ruedenberg, K. In Localization and Delocalization in Quantum Chemistry, Vol. I; Chalvet, O. ; Daudel, R.; Diner, S.; Malrieu, J. P., Eds.; Reidel: Dordrecht, The Netherlands, 1975; pp 223-245.
6. Baird, N. C. J. Chem. Educ. 1986, 63, 660-664.
7. Harcourt, R. D. Am. J. Phys. 1988, 56, 660-661.
8. Nordholm, S. J. Chem. Educ. 1988, 65, 581-584.
9. Bacskay, G. G.; Reimers, J. R.; Nordholm, S. J. Chem. Educ. 1997, 74, 1494-1502.
10. Rioux, F. Chem. Educator 1997, 2(6), S1430-4171(97)06153-2; DOI 10.1007/s00897010153a.
11. Harcourt, R. D.; Solomon, H.; Beckworth, J.; Chislett, L. Am. J. Phys. 1982, 50, 557-559.
12. Kutzelnigg, W. Angew. Chem. Int. Ed. Eng. 1973, 12, 546-562.
13. Melrose, M. P.; Chauhan, M.; Kahn, F. Theor. Chim. Acta 1994, 88, 311-324.
14. Gordon, M. S.; Jensen, J. H. Theor. Chem. Acc. 2000, 103, 248-251.
15. Slater, J. C. J. Chem. Phys. 1933, 1, 687-691.
16. Slater, J. C. Quantum Theory of Matter; Krieger Publishing: Huntington, NY, 1977; pp 405-408.
17. For a thorough discussion of the virial theorem see: Levine, I. N. Quantum Chemistry, 4th ed.; Prentice Hall: Englewood Cliffs, NJ, 1991, Chapter 14.
18. Morse, P. M. Phys. Rev. 1929, 34, 57.
19. Huber, K. P.; Herzberg, G. Molecular Spectra and Molecular Structure, Vol IV; Constants of Diatomic Molecules; Van Nostrand Reinhold: New York, 1979.
20. Winn, J. S. J. Chem. Phys. 1981, 74, 608-611.
21. Kolos, W.; Wolniewicz, L. J. Chem. Phys. 1965, 43, 2429. 22. According to de Broglie, p = h/λ, which means T ∼ λ^-2. Because the wavelength of a confined particle is proportional to the confinement dimension R, we have T ∼ R^-2 and in terms of confinement volume T ∼ V^-2/3.