2.5: The de Broglie-Bohr Model for the Hydrogen Atom - Version 4
- Page ID
- 154850
The 1913 Bohr model of the hydrogen atom was replaced by Schrödingerʹs wave mechanical model in 1926. However, Bohrʹs model is still profitably taught today because of its conceptual and mathematical simplicity, and because it introduced a number of key quantum mechanical ideas such as the quantum number, quantization of observable properties, quantum jump and stationary state.
Bohr calculated the manifold of allowed electron energies by balancing the mechanical forces (centripetal and electron‐nucleus) on an electron executing a circular orbit of radius R about the nucleus, and then arbitarily quantizing its angular momentum. Finally by fiat he declared that the electron was in a non‐radiating stationary state because an orbiting (accelerating) charge radiates energy and will collapse into the oppositely charge nucleus.
In 1924 de Broglie postulated wave‐particle duality for the electron and other massive particles, thereby providing the opportunity to remove some of the arbitariness from Bohrʹs model. For example, an electron possessing wave properties is subject to constructive and destructive interference. As will be shown this leads naturally to quantization of electron momentum and kinetic energy, and consequently a manifold of allowed energy states for the electron relative to the nucleus. The de Broglie‐Bohr model of the hydrogen atom presented here treats the electron as a particle on a ring with wave‐like properties.
\[ \lambda = \frac{h}{m_e v} \nonumber \]
de Broglie's hypothesis that matter has wave-like properties.
\[n \lambda = 2 \pi r \nonumber \]
The consequence of de Broglieʹs hypothesis; an integral number of wavelengths must fit within the circumference of the orbit. This introduces the quantum number which can have values 1,2,3,... The n = 4 electron state is shown below.
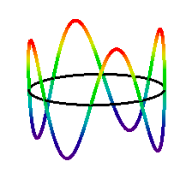
\[ m_e v = \frac{n h }{2 \pi r} \nonumber \]
Substitution of the first equation into the second equation reveals that momentum is quantized.
\[ T = \frac{1}{2} m_e v^2 = \frac{n^2 h^2}{8 \pi^2 m_e r^2} \nonumber \]
If momentum is quantized, so is kinetic energy.
\[ E = T + V = \frac{n^2 h^2}{8 \pi^2 m_e r^2} - \frac{e^2}{4 \pi \varepsilon_0 r} \nonumber \]
Which means that total energy is quantized. The second term is the electron‐proton electrostatic potential energy.
The quantum mechanical interpretation of these ʺBohr orbitsʺ is that they are stationary states. In spite of the fact that we use the expression kinetic energy, which implies electron motion, there is no motion. The electron occupies the orbit as a particle‐wave, it is not orbiting the nucleus. If it was orbiting in a classical sense it would radiate energy and quickly collapse into the nucleus. Clearly the stability of matter requires the quantum mechanical version of kinetic energy.
The ground state energy and orbit radius of the electron in the hydrogen atom is found by plotting the energy as a function of the orbital radius. The ground state is the minimum in the total energy curve. Naturally calculus can be used to obtain the same information by minimizing the energy with respect to the orbit radius. However, the graphical method has the virtue of illuminating the issue of atomic stability.
Fundamental constants: electron charge, electron mass, Planck's constant, vacuum permitivity.
\[ \begin{matrix} e = 1.6021777 (10)^{-19} \text{coul} & m_e = 9.10939 (10)^{-31} \text{kg} \\ h = 6.62608 (10)^{-34} \text{joule sec} & \varepsilon_0 = 8.85419 (10)^{-12} \frac{ \text{coul}^2}{ \text{joule m}} \end{matrix} \nonumber \]
Quantum number and conversion fact between meters and picometers and joules and attojoules.
\[ \begin{matrix} n = 1 & pm = 10^{-12} m & \text{ajoule} = 10^{-18} \text{joule} \end{matrix} \nonumber \]
\[ \begin{matrix} r = 20 pm,~20.5 pm,~ 500 pm & T(r) = \frac{n^2 h^2}{8 \pi^2 m_e r^2} & V(r) = - \frac{e^2}{4 \pi \varepsilon_0 r} & E(r) = T(r) + V(r) \end{matrix} \nonumber \]
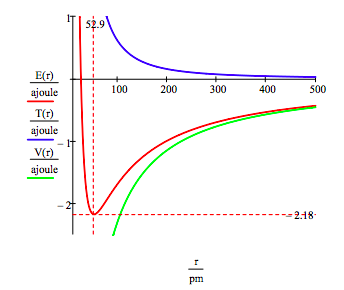
This figure shows that atomic stability involves a balance between potential and kinetic energy. The electron is drawn toward the nucleus by the attractive potential energy interaction (~ ‐1/R), but is prevented from collapsing into the nucleus by the extremely large kinetic energy (~1/R2) associated with small orbits.
As shown below, the graphical approach can also be used to find the electronic excited states.
\[ \begin{matrix} n = 2 & T(r) = \frac{n^2 h^2}{8 \pi^2 m_e r^2} & V(r) = - \frac{e^2}{4 \pi \varepsilon_0 r} & E(r) = T(r) + V(r) \end{matrix} \nonumber \]
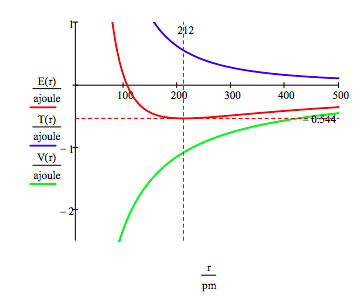
As mentioned earlier the manifold of allowed electron energies can also be obtained by minimizing the energy with respect to the orbit radius. This procedure yields,
\[ \begin{matrix} E_n = - \frac{m_e e^4}{2 \left(4 \pi \varepsilon_0 \right)^2 \hbar^2 } \frac{1}{n^2} & \text{and} & r_n = \frac{4 \pi \varepsilon_0 \hbar^2}{m_e e^2} n^2 \end{matrix} \nonumber \]

