10.37: Hybrid Variational Calculation for the 1D Hydrogen Atom with Delta Function Potential

The following normalized trial wave function is used in a variational calculation for the energy of a one‐dimensional model of the hydrogen atom that postulates a delta‐function potential energy interaction between the electron and the proton. The variational parameter, \( \alpha\), is a decay constant which controls the spatial extent of the wave function.

\[ \Psi (x, \alpha ) = \sqrt{ \alpha} exp( - \alpha |x|) \nonumber \]

\[ \int_{- \infty}^{ \infty} \Psi (x, \alpha)^{2} dx~assume,~ \alpha > 0 \rightarrow 1 \nonumber \]

The Hamiltonian energy operator in coordinate space in atomic units (h/2π = m_e = e = 1) is:

\[ H = \frac{-1}{2} \frac{d^2}{dx^2} \blacksquare - \Delta (x) \blacksquare \nonumber \]

The problem this tutorial seeks to solve is that it is obvious that the coordinate wave function is unsuitable for the calculation of the expectation value for kinetic energy because it is not well‐behaved at x = 0. The wave function and its first and second derivatives are discontinuous at x = 0. In spite of this defect, calculation of the expectation value for potential energy presents no problem in coordinate space.

Therefore the plan is to calculate the potential energy in coordinate space and Fourier transform the coordinate wave function into momentum space, where the wave function is well behaved, for the calculation of kinetic energy. Then the energy will be minimized with respect to \( \alpha\), yielding the following results: \( \alpha\) = 1, E = ‐0.5.

Using several values for x and the optimum value of \( \alpha\) it is shown that solving Schrödingerʹs equation in the coordinate representation for the energy gives the correct value except at the discontinuity, x = 0.

\[ x = 0~~~ \frac{-1}{2} \frac{d^2}{dx^2} \Psi (x, 1) - \Delta (x) \Psi (x, 1) = E \Psi (x, 1)~solve,~E \rightarrow 0 \nonumber \]

\[ x = 2~~~ \frac{-1}{2} \frac{d^2}{dx^2} \Psi (x, 1) - \Delta (x) \Psi (x, 1) = E \Psi (x, 1)~solve,~E \rightarrow \frac{-1}{2} \nonumber \]

\[ x = -1~~~ \frac{-1}{2} \frac{d^2}{dx^2} \Psi (x, 1) - \Delta (x) \Psi (x, 1) = E \Psi (x, 1)~solve,~E \rightarrow \frac{-1}{2} \nonumber \]

Calculation of Potential Energy in Coordinate Space

\[ V( \alpha ) = \int_{- \infty}^{ \infty} \Psi (x, \alpha ) - \Delta (x) \Psi (x, ]alpha ) dx~ \rightarrow - \alpha \nonumber \]

Fourier Transform of the Coordinate Space Wave Function into Momentum Space

\[ \Phi (p, \alpha ) = \int_{- \infty}^{ \infty} \frac{exp(-pix)}{ \sqrt{2 \pi}} \Psi (x, \alpha )dx ~\big|_{simplify}^{assume,~ \alpha > 0} \rightarrow \frac{ \sqrt{2} \alpha ^{ \frac{3}{2}}}{ \sqrt{ \pi} ( \alpha^2 + p^2)} \nonumber \]

Before proceeding, we demonstrate that the momentum space wavefunction is normalized and well behaved.

\[ \int_{ \infty}^{- \infty} \Phi (p, \alpha )^2 dp~assume,~ \alpha > 0 \rightarrow 1 \nonumber \]

The kinetic energy operator in momentum space for an electron is: \( \frac{p^2}{2} \blacksquare\)

Therefore, the kinetic energy is:

\[ T ( \alpha ) = \int_{- \infty}^{ \infty} \Phi (p, \alpha ) \frac{p^2}{2} \Phi (p, \alpha ) dp~ asssume,~ \alpha > 0 \rightarrow \frac{ \alpha ^2}{2} \nonumber \]

Now the coordinate and momentum space calculations are combined and the total energy is minimized with respect to the variational parameter, \( \alpha\).

\[ E ( \alpha ) = T ( \alpha ) + V ( \alpha ) \nonumber \]

\[ \alpha = \frac{d}{d \alpha} E( \alpha ) = 0~solve,~ \alpha \rightarrow 1 \nonumber \]

\[ E ( \alpha ) \rightarrow \frac{-1}{2} \nonumber \]

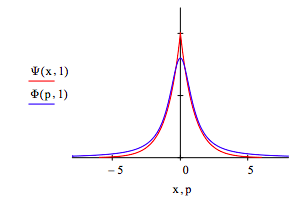
The optimum coordinate and momentum wavefunctions are compared below: x = -6, -5.99 .. 6

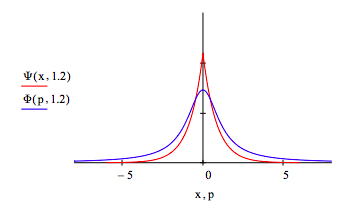
The uncertainty principle is illustrated by displaying the coordinate and momentum wave functions for different values of the decay constant, \( \alpha\). For \( \alpha\) = 1.2 the spatial distribution contracts and the momentum distribution expands relative to the optimum value \( \alpha\) =1. In other words, less uncertainty in position requires greater uncertainty in momentum.

For \( \alpha\) = 0.7 the spatial distribution expands and the momentum distribution contracts. More uncertainty in position leads to less uncertainty in momentum.

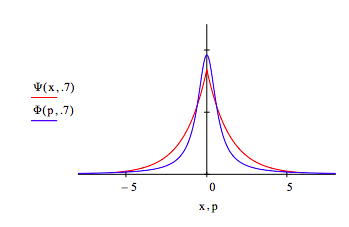
Numerically the Heisenberg uncertainty principle states that the product of the uncertainties in position and momentum must be greater than or equal to 0.5 in atomic units.

\[ \Delta x = \sqrt{ \langle x^2 \rangle - \langle x \rangle^2} \nonumber \]

\[ \Delta p = \sqrt{ \langle x^2 \rangle - \langle x \rangle^2} \nonumber \]

\[ \Delta x \Delta p \geq \frac{h}{2} \nonumber \]

The momentum wave function is now used to verify that the uncertainty principle is satisfied.

\[ \begin{pmatrix}
Operator & Coordinate~Space & Momentum~Space\\
position & x \blacksquare & i \frac{d}{dp} \blacksquare\\
momentum & \frac{1}{i} \frac{d}{dx} \blacksquare & p \blacksquare
\end{pmatrix} \nonumber \]

\[ x_{ave} = \int_{- \infty}^{ \infty} \Phi (p, 1) i \frac{d}{dp} \Phi (p, 1) dp \rightarrow 0 \nonumber \]

\[ x2_{ave} = \int_{- \infty}^{ \infty} \Phi (p, 1) - \frac{d}{dp} \Phi (p, 1) dp \rightarrow \frac{1}{2} \nonumber \]

\[ p_{ave} = \int_{- \infty}^{ \infty} \Phi (p, 1)^2 dp \rightarrow 0 \nonumber \]

\[ p2_{ave} = \int_{- \infty}^{ \infty} p^2 \Phi (p, 1)^2 dp \rightarrow 1 \nonumber \]

\[ \sqrt{x2_{ave} - x_{ave}^2} \sqrt{p2_{ave} - p_{ave}^2} = 0.707 \nonumber \]

Concluding Remarks

This hybrid variational calculation on a one‐dimensional model of the hydrogen atom using a delta function potential interaction between the proton and electron yields the correct ground state energy. The model is composed of two peculiar elements: a trial wave function that has discontinuity at x = 0 and a potential energy interaction that is zero everywhere except at x = 0.

In Molecular Quantum Mechanics, 3rd ed., p. 43 Atkins and Friedman list the following criteria for an acceptable wave function.

1. It must be single valued (strictly Ψ*Ψ must be single valued).
2. It must not be infinite over a finite range.
3. It must be continuous everywhere.
4. It must have a continuous first derivative, except at ill‐behaved regions of the potential.

Ψ(x,α) does not satisfy criterion 3, making it impossible to calculate kinetic energy in the coordinate representation. However, it does satisfy criterion 4, so it is possible to calculate potential energy in the coordinate representation. Φ(p,α) is well‐behaved for all values of p. It is used to calculate kinetic energy, but it is not suitable for the calculation of potential energy. Thatʹs why a hybrid variational calculation was used.