10.32: Momentum-Space Variation Method for the Abs(x) Potential

The energy operator in atomic units in coordinate space for a unit mass particle with potential energy V = |x| is given below.

\[ H = \frac{-1}{2} \frac{d^2}{dx^2} \blacksquare + |x| \blacksquare \nonumber \]

Suggested trial wave function:

\[ \Psi (x, \beta ) := ( \frac{2 \beta}{ \pi})^{ \frac{1}{4}} exp(- \beta x^2) \nonumber \]

Demonstrate that the wave function is normalized.

\[ \int_{- \infty}^{ \infty} \Psi (x, \beta )^2 dx~~assume,~ \beta >0 \rightarrow 1 \nonumber \]

Carry out Fourier transform to get momentum wave function:

\[ \Phi (p, \beta ) := \frac{1}{ \sqrt{2 \pi}} \int_{- \infty}^{ \infty} exp(-ipx) \Psi (x, \beta ) dx |_{simplify}^{assume,~ \beta > 1} \rightarrow \frac{1}{2} \frac{2^{ \frac{3}{4}}}{ \pi ^{ \frac{1}{4}}} \frac{e^{\frac{-1}{4}} \frac{p^2}{ \beta}}{ \beta ^{ \frac{1}{4}}} \nonumber \]

Demonstrate that the momentum wave function is normalized.

\[ \int_{- \infty}^{ \infty} \overline{ \Phi (p, \beta )} \Phi (p, \beta ) dp~~~assume,~ \beta > 0 \rightarrow 1 \nonumber \]

The energy operator in momentum space is:

\[ H = \frac{p^2}{2} \blacksquare + |i + \frac{d}{dp} \blacksquare| \nonumber \]

Evaluate the variational energy integral:

\[ E( \beta ) := \int_{- \infty}^{ \infty} \overline{ \Phi (p, \beta )} \frac{p^2}{2} \Phi (p, \beta ) dp + \int_{- \infty}^{ \infty} \overline{ \Phi (p, \beta )} |i \frac{d}{dp} \Phi (p , \beta )| dp |_{simplify}^{assume,~ \beta >0} \frac{1}{2} \frac{ \pi^{ \frac{1}{2}} \beta^{ \frac{3}{2}} + 2^{ \frac{1}{2}}}{ \beta^{ \frac{1}{2}} \pi^{ \frac{1}{2}}} \nonumber \]

Minimize the energy with respect to the variational parameter β and report its optimum value and the ground-state energy.

\( \beta\) := 1 \( \beta\) := Minimize (E, \( \beta\)) \( \beta\) = 0.542 E( \( \beta\)) = 0.813

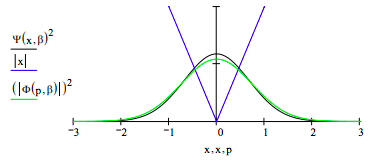
Plot the coordinate and momentum wave functions and the potential energy on the same graph.