10.26: Trigonometric Trial Wavefunction for the Helium Atom

Last updated
Save as PDF

Page ID: 136976

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Trigonometric trial wavefunction:

\[ \psi (r, \beta ) = \sqrt{ \dfrac{3 \beta ^3}{ \pi ^3}} \text{sech}( \beta r) \nonumber \]

Demonstrate the wavefunction is normalized.

\[ \int_{0}^{\infty} \psi (r, \beta )^2 4 \pi r^2 dr |_{simplify}^{assume,~ \beta >0} \nonumber \]

The terms contributing to the total electronic energy of the helium atom are the kinetic energy of each electron, each electronʹs interaction with the nucleus, and the interaction of the electrons with each other.

Calculate kinetic energy:

\[ 2 \int_{0}^{ \infty} \psi (r, \beta ) \left[ \frac{-1}{2r} \frac{d^2}{dr^2} (r \psi (r, \beta )) \right] 4 \pi r^2 dr |_{simplify}^{assume,~ \beta >0} \rightarrow \frac{1}{3} \beta ^2 \frac{12 + \pi^2}{ \pi^2} \nonumber \]

Calculate electron-nucleus potential energy:

\[ 2 \int_{0}^{ \infty} \psi (r, \beta ) \frac{-2}{r} \psi (r, \beta ) 4 \pi r^2 dr |_{simplify}^{assume,~ \beta > 0} \rightarrow (-48) \beta \frac{\ln(2)}{ \pi ^2} \nonumber \]

Calculate electron-electron potential energy:

\[ \int_{0}^{ \infty} \psi (r, \beta )^2 \left( \frac{1}{r} \int_{0}^{r} \psi (x, \beta )^2 4 \pi x^2 dx + \int_{r}^{ \infty} \frac{ \psi (x, \beta )^2 4 \pi x^2}{x} dx \right) 4 \pi r^2 dr \nonumber \]

Write the equation for the total electronic energy in terms of the variational parameter \( \beta\):

\[ E( \beta ) = \frac{1}{3} \beta ^2 \frac{12 + \pi ^2}{ \pi ^2} + (-48) \beta \frac{\ln(2)}{ \pi ^2} + \int_{0}^{ \infty} \psi (r, \beta )^2 \left( \frac{1}{r} \int_{0}^{r} \psi (x, \beta )^2 4 \pi x^2 dx + \int_{r}^{ \infty} \frac{ \psi (x, \beta )^2 4 \pi x^2}{x}\right) 4 \pi r^2 dr \nonumber \]

Minimize the energy with respect to the variational parameter \( \beta\).

\( \beta\) = 1 \( \beta\) = Minimize(E, \( \beta\) \( \beta\) = 1.902 E( \( \beta\) = -2.672

Compare the variational calculation to the Hartree-Fock limit: \(E_{HF} = -2.8617\)

\[ \frac{E_{HF} - E( \beta )}{E_{HF}} = 6.614 \nonumber \]

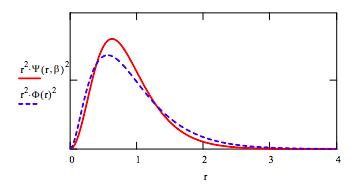
Compare optimized trial wavefunction with the Hartree-Fock wavefunction (see McQuarrie and Simon, page 283) by plotting the radial distribution functions.

\[ \Phi (r) = 0.75738\exp(1.430r) + 0.43658 \exp(-2.4415r) + 0.17295 \exp (-4.0996r) − 0.02730 \exp (-6.4843r) + 0.06675 \exp (7.97) \nonumber \]

Screen Shot 2019-02-14 at 12.53.44 PM.png