10.20: Gaussian Trial Wavefunction for the Hydrogen Atom
- Page ID
- 136259
A Gaussian function, exp(‐αr2), is proposed as a trial wavefunction in a variational calculation on the hydrogen atom. Determine the optimum value of the parameter α and the ground state energy of the hydrogen atom. Use atomic units: h = 2π, me = 1, e = ‐1.
\[ \Phi (r, \beta ) := ( \frac{2 \beta}{ \pi})^{ \frac{3}{4}} exp(- \beta r^2) \nonumber \]
\[ T = \frac{-1}{2r} \frac{d^2}{dr^2} (r \blacksquare ) \nonumber \]
\[ V = \frac{1}{r} \nonumber \]
\[ \int_{0}^{ \infty} \blacksquare 4 \pi r^2 dr \nonumber \]
a. Demonstrate the wave function is normalized.
\[ \int_{0}^{ \infty} \Psi (r, \beta )^2 4 \pi r^2 dr |_{simplify}^{assume,~ \beta >0} \rightarrow 1 \nonumber \]
b. Evaluate the variational integral.
\[ E ( \beta ) := \int_{0}^{ \infty} \Psi (r, \beta ) [ \frac{-1}{2r} \frac{d^2}{dr^2} (r \Psi (r, \beta ))] 4 \pi r^2 dr ... |_{simplify}^{assume,~ \beta >0} \rightarrow \frac{1}{2} \frac{3 \pi^{\frac{1}{2}} \beta - (4) 2^{ \frac{1}{2}} \beta^{ \frac{1}{2}}}{ \pi^{ \frac{1}{2}}} + \int_{0}^{ \infty} \Psi (r, \beta ) \frac{-1}{r} \Psi (r, \beta ) 4 \pi r^2 dr \nonumber \]
c. Minimize the energy with respect to the variational parameter \( \beta\).
\( \beta\) := 1 \( \beta\) := Minimize (E, \( \beta\)) \( \beta\) = 0.283 E( \( \beta\)) = -0.424
d. The exact ground state energy for the hydrogen atom is -.5 Eh. Calculate the percent error.
\[ \frac{-.5 - E( \beta )}{-.5} = 15.117 \nonumber \]
e. The differences between the Gaussian and Slate type wavefunctions are illustrated with the surface plots shown below.
N := 50 b := 5 i := 0..N j := 0..N \( y_{i} := -b + \frac{2bi}{N}\) \( x_{j} := -b + \frac{2bj}{N}\)
\[ Gauss_{i,~j} := ( \frac{2 \beta}{ \pi})^{ \frac{3}{4}} exp[- \beta [ (x_{i})^2 + (y_{j})^2]] \nonumber \]
\[ Slater_{i,~j} := \frac{1}{ \sqrt{ \pi}} exp [ - \sqrt{ (x_{i})^2 + (y_{j})^2}] \nonumber \]

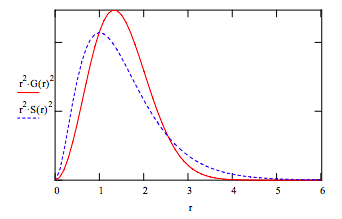
f. These wavefunctions can also be compared to their radial distribution functions:
r := 0, .1 .. 6
\[ G(r) := ( \frac{2 \beta}{ \pi}) ^{ \frac{3}{4}} exp( - \beta r^2) \nonumber \]
\[ S(r) := \frac{1}{ \sqrt{ \pi}} exp( -r ) \nonumber \]