10.19: Trigonometric Trial Wave Function for the 3D Harmonic Potential Well
- Page ID
- 136258
Trial wave function: \( \Psi (r, \beta) := \sqrt{ \frac{3 \beta^3}{ \pi^3}} sech( \beta r)\)
Integral: \( \int_{0}^{ \infty} \blacksquare 4 \pi r^2 dr\)
Kinetic energy operator: \( T = \frac{-1}{2r} \frac{d^2}{dr^2} (r \blacksquare )\)
Potential energy operatory: \( V = \frac{1}{2} k r^2\)
a. Demonstrate the wave function is normalized.
\( \int_{0}^{ \infty} \Psi (r, \beta )^2 4 \pi r^2 dr |_{simplify}^{assume,~ \beta > 0} \rightarrow 1\)
b. Evaluate the variational integral.
\( E( \beta ) := \int_{0}^{ \infty} \Psi (r, \beta ) [ \frac{-1}{2r} \frac{d^2}{dr^2} (r \Psi (r, \beta ))] 4 \pi r^2 dr + \int_{0}^{ \infty} \Psi (r, \beta ) \frac{1}{2} r^2 \Psi (r, \beta ) 4 \pi r^2 dr\)
c. Minimize the energy with respect to the variational parameter \( \beta\).
\( \beta\) := 1 \( \beta\) := Minimize (E, \( \beta\)) \( \beta\) = 1.471 E( \(\beta \)) = 1.597
d. The exact ground state energy for the 3D harmonic oscillator is 1.5 Eh. Calculate the percent error.
\( \frac{E( \beta ) - 1.5}{1.5} = 6.488\)%
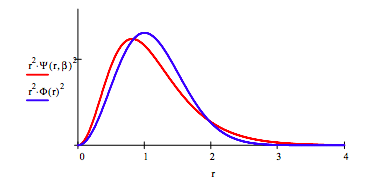
e. Compare the optimized trial wave function with the exact solution by plotting the radial distribution functions.
\( \Phi (r) := ( \frac{1}{ \pi})^{ \frac{3}{4}} exp( \frac{r^2}{2})\)
h. Calculate the overlap integral between the trial wave function and the exact wave function.
\( \int_{0}^{ \infty} \Psi (r, \beta ) \Phi (r) 4 \pi r^2 dr = 0.989\)
i. Calculate the probability that tunneling is occurring.
Classical turning point:
\( 1.597 = \frac{1}{2} r^2 |_{float,~3}^{solve,~r} \rightarrow {\begin{pmatrix}
-1.79 \\
1.79
\end{pmatrix}}\)
Tunneling probability:
\( \int_{1.79}^{ \infty} \Psi (r, \beta )^2 4 \pi r^2 dr = 12.598\)%

