10.17: Variation Method for the Harmonic Oscillator

Last updated
Save as PDF

Page ID: 136255

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

This exercise deals with a variational treatment for the ground state of the simple harmonic oscillator which is, of course, an exactly soluble quantum mechanical problem.

The energy operator for a harmonic oscillator with unit effective mass and force constant is:

\( H = \frac{-1}{2} \frac{d^2}{dx^2} \blacksquare + \frac{x^2}{2} \blacksquare\)

The following trial wavefunction is selected:

\[ \psi (x, \beta ) = \frac{1}{1 + \beta x^2} \nonumber \]

The variational energy integral is evaluated (because of the symmetry of the problem it is only necessary to integrate from 0 to ∞, rather than from ‐∞ to ∞:

\( E( \beta ) = \dfrac{ \int_{0}^{ \infty} \psi (x, \beta ) \frac{-1}{2} \frac{d^2}{dx^2} \psi (x, \beta ) dx + \int_{0}^{ \infty} \psi (x, \beta ) \frac{x^2}{2} \psi (x, \beta ) dx}{ \int_{0}^{ \infty} \psi (x, \beta )^2 dx} |^{assume,~ \beta > 0}_{simplify} \rightarrow \frac{1}{4} \frac{ \beta ^2 + 2}{ \beta}\)

The energy integral is minimized with respect to the variational parameter:

\( \beta \) := 1 \( \beta \) := Minimize (E, \( \beta\)) \( \beta\) = 1.414 E( \(\beta\)) = 0.707

The % error is calculated given that the exact result is \(0.50 E_h\).

\( \frac{E( \beta ) - 0.5}{0.5} = 41.421\)%

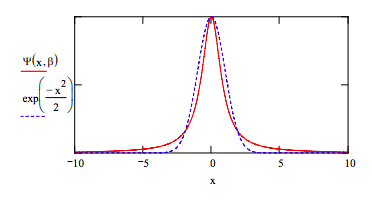
The optimized trial wavefunction is compared with the SHO ground-state eigenfunction.

Screen Shot 2019-02-12 at 12.50.41 PM.png

Now a second trial function is chosen:

\( \psi (x, \beta ) := \frac{1}{(1 + \beta x^2)^2}\)

Evaluate the variational energy integral:

\( E( \beta ) := \frac{ \int_{0}^{ \infty} \psi (x, \beta ) \frac{-1}{2} \frac{d^2}{dx^2} \psi (x, \beta ) dx + \int_{0}^{ \infty} \psi (x, \beta ) \frac{x^2}{2} \psi (x, \beta ) dx}{ \int_{0}^{ \infty} \psi (x, \beta )^2 dx} |^{assume,~ \beta > 0}_{simplify} \rightarrow \frac{1}{10} \frac{7 \beta ^2 + 1}{ \beta}\)

Minimize the energy integral with respect to the variational parameter:

\( \beta \) := 1 \( \beta \) := Minimize (E, \( \beta\)) \( \beta\) = 0.378 E( \(\beta\)) = 0.529

Calculate the % error given that the exact result is 0.50 E_h.

\( \frac{E( \beta ) - 0.5}{0.5} = 5.83\)%

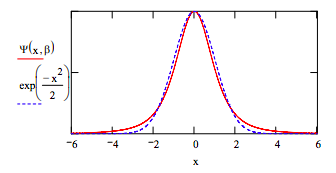
The optimized trial wavefunction is compared with the SHO ground-state eigenfunction.

Screen Shot 2019-02-12 at 12.50.36 PM.png

Suggestion: Continue this exercise with the following trial wavefunction and interpret the improved agreement with the exact solution.

\( \psi (x, \beta ) - \frac{1}{(1 + \beta x^2)^n}\)

where n is an integer greater than 2.