10.16: Variation Method for a Particle in a Finite 3D Spherical Potential Well
- Page ID
- 136254
This problem deals with a particle of unit mass in a finite spherical potential well of radius 2 ao and well height 2 Eh. The trial wave function is given below.
\[ \psi (r, \beta ) := ( \frac{2 \beta}{ \pi})^{ \frac{3}{4}} exp(- \beta r^2) \nonumber \]
\[ T = - \frac{1}{2r} \frac{d^2}{dr^2} (r \blacksquare ) \nonumber \]
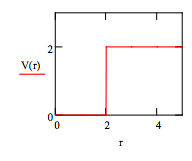
\( V(r) := if [(r \leq 2), 0, 2]\)
a. Demonstrate that the wave function is normalized.
\[ \int_{0}^{ \infty} \psi (r, \beta )^2 4 \pi r^2 dr |_{simplify}^{assume,~ \beta > 0} \rightarrow 1 \nonumber \]
b. Evaluate the variational integral.
\[ E( \beta ) := \int_{0}^{ \infty} \psi (r, \beta ) [- \frac{1}{2r} \frac{d^2}{dr^2} (r \psi (r, \beta ))] 4 \pi r^2 dr ... |_{simplify}^{assume,~ \beta > 0} + \int_{2}^{ \infty} 2 \psi (r, \beta )^2 4 \pi r^2 dr \nonumber \]
\[ E( \beta ) := \frac{1}{2} \frac{3 \pi^{ \frac{1}{2}} \beta + 4 \pi ^{ \frac{1}{2}} + 16 exp(-8 \beta) 2^{ \frac{1}{2}} \beta^{ \frac{1}{2}}-4 \pi ^{\frac{1}{2}} erf((2) 2^{ \frac{1}{2}} \beta^{ \frac{1}{2}}) }{ \pi ^{ \frac{1}{2}}} \nonumber \]
c. Minimize the energy with respect to the variational parameter \( \beta\).
\( \beta\) := 5 \( \beta\) := Minimize (E, \beta ) \( \beta\) = 0.381 \( E ( \beta ) = 0.786\)
d. Calculate the average value of r.
\( \int_{0}^{ \infty} r \psi (r, \beta )^2 4 \pi r^2 dr = 1.293\)
e. Calculate the kinetic and potential energy.
Potential energy:
\( \int_{2}^{ \infty} r \psi (r, \beta )^2 4 \pi r^2 dr = 0.215\)
Kinetic energy:
\( E( \beta ) - 0.215 = 0.571\)
f. Calculate the probability that the particle is in the barrier.
\( 1 - \int_{0}^{2} \psi (r, \beta )^2 4 \pi r^2 dr = 0.107\)
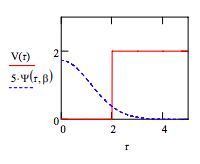
g. Plot the wavefunction on the same graph as the potential energy.