10.15: Variation Method for a Particle in an Ice Cream Cone
- Page ID
- 136253
A Gaussian function is proposed as a trial wavefunction in a variational calculation for a particle experiencing a linear radial potential energy. Determine the optimum value of the parameter β and the optimum ground state energy. Use atomic units: h = 2π, me = 1, e = ‐1.
\[ \psi (r, \beta ) := ( \frac{2 \beta}{ \pi})^{ \frac{3}{4}} exp(- \beta r^2) \nonumber \]
\[ T = \frac{1}{2r} \frac{d^2}{dr^2} (r \blacksquare ) \nonumber \]
\[ V = r \nonumber \]
\[ \int_{0}^{ \infty} \blacksquare 4 \pi r^2 dr \nonumber \]
a. Demonstrate the wave function is normalized.
\[ \int_{0}^{ \infty} \psi (r, \beta )^2 4 \pi r^2 dr |_{simplify}^{assume,~ \beta >0} \rightarrow 1 \nonumber \]
b. Evaluate the variational integral.
\[ E( \beta ) := \int_{0}^{ \infty} \psi (r, \beta [ (- \frac{1}{2r}) \frac{d^2}{dr^2} (r \psi (r, \beta))] 4 \pi r^2 dr ... |_{simplify}^{assume,~ \beta > 0} \rightarrow \frac{1}{2} \frac{3 \pi^{ \frac{1}{2}} \beta^2 + (2)2^{ \frac{1}{2}} \beta ^{ \frac{1}{2}}}{ \pi^{ \frac{1}{2}} \beta} \nonumber \]
c. Minimize the energy with respect to the variational parameter \( \beta\).
\( \beta\) := 1 \( \beta\) := Minimize(E, \beta ) \( \beta\) = 0.414 E( \( \beta\)) = 1.861
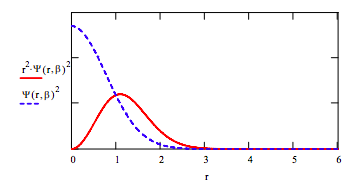
d. Plot the optimized trial wave function.