10.14: Variation Method for a Particle in a 1D Ice Cream Cone

Last updated
Save as PDF

Page ID: 136251

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Define potential energy: V(x) := |x|

Display potential energy:

Screen Shot 2019-02-12 at 11.52.28 AM.png

Choose trial wave function: \( \Psi (x, \beta ) := \sqrt{ \frac{ \beta}{2}} sech( \beta x)\)

\[ E ( \beta ) := \int_{- \infty}^{ \infty} \Psi (x, \beta ) \frac{1}{2} \frac{d^2}{dx^2} \Psi (x, \beta ) dx + \int_{- \infty}^{ \infty} V(x) \Psi (x, \beta )^{2} dx \nonumber \]

Minimize the energy integral with respect to the variational parameter, \( \beta\).

\( \beta\) := 2 \( \beta\) := Minimize( E, \( \beta\)) \( \beta\) = 1.276 E( \(\beta\)) = 0.815

Display wave function in the potential well.

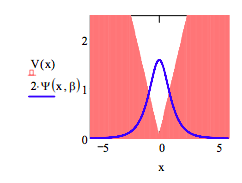
Screen Shot 2019-02-12 at 11.52.33 AM.png

Calculate the probability that the particle is in the potential barrier.

\[ 2 \int_{0}^{ \infty} \Psi (x, \beta )^2 dx = 1 \nonumber \]

Define quantum mechanical tunneling.

Tunneling occurs when a quon (a quantum mechanical particle) has probability of being in a nonclassical region. In other words, a region in which the total energy is less than the potential energy.

Calculate the probability that tunneling is occurring.

\[ |x| = 0.815 |_{float,~4}^{solve,~x} \rightarrow {\begin{pmatrix}
0.8150 \\
-0.8150
\end{pmatrix}} \nonumber \]

\[ 2 \int_{0.815}^{ \infty} \Psi (x, \beta )^2 dx = 0.222 \nonumber \]

Calculate the kinetic and potential energy contributions to the total energy.

Kinetic energy:

\[ \int_{- \infty}^{ \infty} \Psi (x, \beta ) -( \frac{1}{2}) \frac{d^2}{dx^2} \Psi (x, \beta ) dx = 0.272 \nonumber \]

Potential energy:

\[ \int_{- \infty}^{ \infty} V(x) \Psi (x, \beta )^{2} dx = 0.543 \nonumber \]