10.12: Variation Method for a Particle in a Semi-Infinite Potential Well
- Page ID
- 136124
This problem deals with the variational approach to the particle in the semi-infinite potential well.
Kinetic energy operator: \( - \frac{1}{2} \frac{d^2}{dx^2} \blacksquare\)
Integral: \( \int_{0}^{ \infty} \blacksquare dx\)
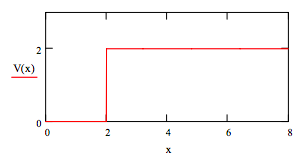
Potential energy: \( V(x) := if[( x \leq 2), 0 , 2]\)
Trial wave function: \( \Phi (x, \beta ) := 2 \beta ^{ \frac{3}{2}}~x~exp(- \beta x)\)
If the trial wave function is not normalized, normalize it.
\( \int_{0}^{ \infty} \Phi (x, \beta )^{2} dx~ assume,~ \beta > 0 \rightarrow 1\)
Evaluate the variational energy integral.
\( E( \beta ) := \int_{0}^{ \infty} \Phi (x, \beta ) (- \frac{1}{2}) \frac{d^2}{dx^2} \Phi (x, \beta ) dx ... |_{simplify}^{assume,~ \beta >0} \rightarrow \frac{1}{2} \beta^{2} + 16 \beta^{2} e^{-4 \beta} + 8 \beta e^{-4 \beta} + 2 e^{- 4 \beta} + \int_{2}^{ \infty} 2 \Phi (x, \beta )^{2} dx\)
Minimize the energy with respect to \( \beta\):
\( \beta\) := .3 \( \beta\) := Minimize \((E, \beta )\) \( \beta = 1.053\) \( E( \beta ) = 0.972\)
Display optimized trial wave function and potential energy:

Calculate average position and most probable position of the particle:
\( \int_{0}^{ \infty} x \Phi (x, \beta )^{2} dx = 1.425\)
\( \frac{d}{dx} \Phi (x, \beta ) = 0 |_{solve,~x}^{float,~3} \rightarrow \frac{1}{ \beta} = 0.95\)
Calculate the probability of the particle in the barrier.
\( \int_{2}^{ \infty} \Phi (x, \beta )^{2} dx = 20.891%\)
Calculate the potential energy, and the kinetic energy.
\( V := \int_{2}^{ \infty} 2 \Phi (x, \beta )^{2} dx\) \(V = 0.418\)
\( T := E ( \beta ) - V\) \( T = 0.554\)

