10.11: Linear Variational Method for a Particle in a Slanted 1D Box

Last updated
Save as PDF

Page ID: 136123

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Trial wavefunctions:

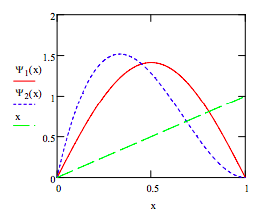
\( \psi_{1} (x) = \sqrt{2} \sin( \pi x)\)
\( \psi_{2} (x) = \sqrt{105} x (1-x)^{2}\)

Plot trial wavefunctions and potential energy. x = 0, .005 ... 1

Screen Shot 2019-02-11 at 1.02.14 PM.png

Evaluate matrix elements:

\[\begin{align} S_{11} &= \int_{0}^{1} \psi _{1} (x)^{2} dx \\[4pt] &= 1 \end{align} \nonumber \]

\[\begin{align} S_{12} &= \int_{0}^{1} \psi _{1} (x) \psi _{2} (x) dx\\[4pt] &= 0.9347 \end{align} \nonumber \]

\[\begin{align} S_{22} &= \int_{0}^{1} \psi _{2} (x)^{2} dx \\[4pt] &= 1 \end{align} \nonumber \]

\( H_{11} = \int_{0}^{1} \psi _{1} (x) (- \frac{1}{2}) \frac{d^{2}}{dx^{2}} \psi _{1} (x) dx + \int_{0}^{1} \psi _{1} (x)~x~ \psi _{1} (x) dx\) \( H_{11} = 5.4348\)

\( H_{12} = \int_{0}^{1} \psi _{1} (x) (- \frac{1}{2}) \frac{d^{2}}{dx^{2}} \psi _{2} (x) dx + \int_{0}^{1} \psi _{1} (x)~x~ \psi _{2} (x) dx\) \( H_{12} = 5.0163\)

\( H_{22} = \int_{0}^{1} \psi _{2} (x) (- \frac{1}{2}) \frac{d^{2}}{dx^{2}} \psi _{2} (x) dx + \int_{0}^{1} \psi _{2} (x)~x~ \psi _{2} (x) dx\) \( H_{22} = 7.375\)

Solve the secular equations and normalization constraint for the energy and coefficients.

Seed values for energy and coefficients: E = 5 c₁ = .5 c₂ = .5

Given

\( (H_{11} - E S_{11})c_{1} + (H_{12} - E S_{12})c_{2} = 0\)

\( (H_{12} - E S_{12})c_{1} + (H_{22} - E S_{22})c_{2} = 0\)

\( c_{1}^{2} S_{11} + 2 c_{1} c_{2} S_{12} + c_{2}^{2} S_{22} = 1\)

\({\begin{pmatrix}
E \\
c_{1} \\
c_{2}
\end{pmatrix}} = Find(E, c_{1}, c_{2})\)

\({\begin{pmatrix}
E \\
c_{1} \\
c_{2}
\end{pmatrix}} = {\begin{pmatrix} 5.4328 \\
0.971\\
0.031
\end{pmatrix}}\)

Compare variational ground state to PIB ground state:

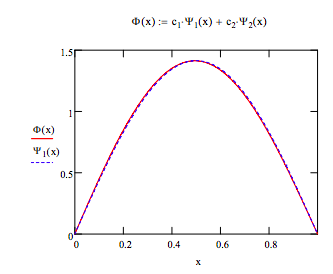
Screen Shot 2019-02-11 at 1.06.01 PM.png

Calculate average position of the particle in the box:

\[ \int_{0}^{1} x \Phi (x)^{2} dx = 0.496 \nonumber \]

Calculate the probability that the particle is in the left half of the box:

\[ \int_{0}^{0.5} \Phi (x)^{2} dx = 0.5088 \nonumber \]