10.10: Variation Method for a Particle in a Gravitational Field

Last updated
Save as PDF

Page ID: 136122

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The particle of unit mass in a gravitational field for which g = 1 has the energy operator shown below.

\( - \frac{1}{2} \frac{d^2}{dz^2} \blacksquare + z \blacksquare\)

\( \int_{0}^{ \infty} \blacksquare dz\)

The following trial wave function for this problem is:

\( \Phi ( \alpha, z) := 2 ( \frac{2 \alpha}{ \pi ^{ \frac{1}{3}}})^{ \frac{3}{4}} z~exp ( - \alpha z^{2})\)

Determine whether or not the wave function is normalized.

\( \int_{0}^{ \infty} \Psi ( \alpha , z)^{2} dz |_{simplify}^{assume,~ \alpha > 0} \rightarrow 1\)

Evaluate the variational energy integral.

\( E ( \alpha ) := \int_{0}^{ \infty} \Psi ( \alpha , z) - \frac{1}{2} \frac{d^2}{dz^2} \Phi ( \alpha , z) dz ... |_{simplify}^{assume,~ \alpha >0} \rightarrow \frac{1}{2 \pi ^{ \frac{1}{2}}} \frac{3 \pi ^{ \frac{1}{2}} \alpha ^{2} + 2 (2)^{ \frac{1}{2}} \alpha ^{ \frac{1}{2}}}{ \alpha} + \int_{0}^{ \infty} z \Psi ( \alpha , z)^{2} dz\)

Minimize the energy with respect to the variational parameter \( \alpha\) and report its optimum value and the ground‐state energy.

\( \alpha := 1\) \( \alpha := Minimize(E, \alpha )\) \( \alpha = 0.4136\) \( E( \alpha ) = 1.8611\) \( E_{exact} := 1.8558\)

Plot the wave function with the distance of the particle from the surface on the vertical axis.

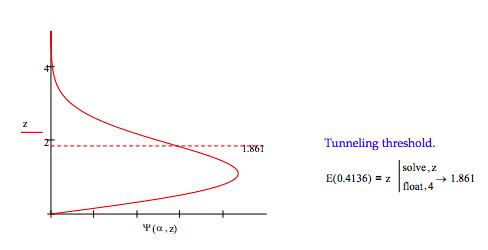
Screen Shot 2019-02-11 at 12.53.15 PM.png

Find that distance below which there is a 90% probability of finding the particle.

\( \alpha := 1\)

Given \( \int_{0}^{a} \Psi ( \alpha , z)^{2} dz = .90\)

Find (a) = 1.9440

Find the most probable value of the position of the particle from the surface.

\( \frac{d}{dz} \Psi (0.4136, z) = 0 |_{float,~3}^{solve,~z} \rightarrow {\begin{pmatrix}
-1.10 \\
1.10
\end{pmatrix}}\)

Calculate the probability that the particle will be found below the most probable distance from the surface.

\( \int_{0}^{1.10} \Psi ( \alpha , z)^{2} dz = 0.4279\)

Calculate the probability that tunneling is occurring: \( \int_{1.861}^{ \infty} \Psi ( \alpha , z)^{2} dz = 0.1256\)

Kinetic energy: \( \int_{0}^{ \infty} \Psi ( \alpha , z) - \frac{1}{2} \frac{d^2}{dz^2} \Psi ( \alpha , z) dz = 0.6204\)

Potential energy: \( \int_{0}^{ \infty} z \Psi ( \alpha , z)^{2} dz = 1.2407\)

What is the apparent virial theorem for this system: \( E = 3T = \frac{3}{2} V\)