Skip to main content
Chemistry LibreTexts

10.5: Variational Method for a Particle in a Finite Potential Well

  1. Last updated
  2. Save as PDF
  • Page ID
    135911

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Definite potential energy: \( V(x) := if [(x \geq -1) \cdot (x \leq 1), 0, 2]\)

    Display potential energy:

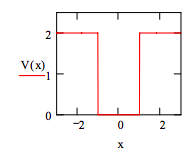
    Screen Shot 2019-02-08 at 11.27.19 AM.png

    Choose trial wavefunction: \( \psi (x, \beta ) := ( \frac{2 \cdot \beta}{ \pi} )^{ \frac{1}{4}} \cdot (- \beta \cdot x^{2})\)

    Demonstrate that the trial wavefunction is normalized.

    \( \int_{- \infty}^{ \infty} \psi (x, \beta )^{2} dx\) assume, \( \beta > 0 \rightarrow 1\)

    Evaluate the variational integral:

    \( E( \beta ) := \int_{- \infty}^{ \infty} \psi (x, \beta ) \cdot - \frac{1}{2} \cdot \frac{d^{2}}{dx^{2}} \psi (x, \beta ) dx ... |_{simplify}^{assume,~ \beta > 0} \rightarrow \frac{1}{2} \cdot \beta + 2 - 2 \cdot erf(2^{ \frac{1}{2}} \cdot \beta^{ \frac{1}{2}})\)

    Minimize the energy integral with respect to the variational parameter, \( \beta\).

    \( \beta\) := 1 \( \beta\) := Minimize(E, \( \beta\)) \( \beta\) = 0.678 E( \( \beta\)) = 0.538

    Display wavefunction in the potential well and compare result with the exact energy, 0.530 Eh.

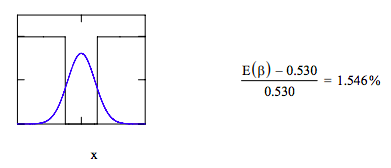
    Screen Shot 2019-02-08 at 11.30.26 AM.png

    Calculate the fraction of time tunneling is occurring.

    \( 2 \cdot \int_{1}^{ \infty} \psi (x, \beta )^{2} dx = 0.1\)

    This page titled 10.5: Variational Method for a Particle in a Finite Potential Well is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Frank Rioux via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.