10.4: A Rudimentary Model for Alpha Particle Decay

Last updated
Save as PDF

Page ID: 135910

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Simple models for the potential energy experienced by an alpha particle in a nucleus have the form shown below. In the interest of mathematical simplicity we will not attempt to model any particular alpha emitter, but just try to capture the essentials of the quantum mechanical tunneling mechanism for alpha decay that was formulated by Gamov, Gurney and Condon in 1928.

\[ V(x) := if[(x \geq 2), 0, \frac{5}{x} ] \nonumber \]

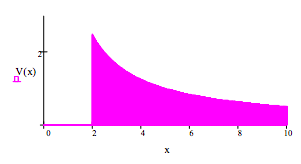
Screen Shot 2019-02-08 at 11.12.04 AM.png

The attractive nuclear interaction (strong nuclear force) is represented by a well of depth 2.5 and range 2 in atomic units. The repulsive Coulomb interaction becomes dominant as the strong nuclear force fades for \(x\) values greater than 2. The trapped particle is assumed to have unit mass. A variational calculation will be carried out using the trial wavefunction given below. It is also possible to solve Schrödinger's equation for alpha decay by numerical integration.

Normalized trial wavefunction with variational parameter \(α\), a decay constant:

\[ \psi (x, \alpha ) := 2 \alpha^{ \frac{3}{2}} x e^{- \alpha x} \nonumber \]

\[ \int_{0}^{ \infty} \psi (x, \alpha )^{2} dx |_{simplify}^{assume,~ \alpha > 0} \rightarrow 1 \nonumber \]

Set up the variational energy integral:

\[ E ( \alpha ) := \int_{0}^{ \infty} \psi (x, \alpha ) \frac{1}{2} \frac{d^{2}}{dx^{2}} \psi (x, \alpha ) dx + \int_{0}^{ \infty} V(x) \psi (x, \alpha )^{2} dx \nonumber \]

Next the energy is minimized with respect to \(α\) numerically. This method requires a seed value for \(α\).

α := 3 α := Minimize(E, α) α:= 1.003 E(α) = 0.958

In what follows the results of the variational calculation will be displayed graphically and interpreted.

Display the results of the variational calculation:

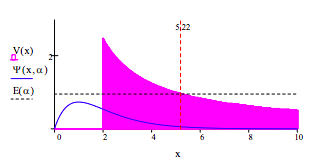
Screen Shot 2019-02-08 at 11.12.12 AM.png

Calculate the probability that the particle is in the classically forbidden region. This is the region where the particle's total energy is less than the potential energy.

Because the energy of the particle is 0.958, the classical forbidden region extends from \(x = 2\) to \(x = 5.22\).

\[ \frac{5}{x} = 0.958 |_{solve,~x}^{float,~3} \rightarrow 5.22 \nonumber \]

Probability in classically forbidden region:

\[ \int_{2}^{5.22} \psi (x, \alpha )^{2} dx = 0.234 \nonumber \]

Calculate the probability that the particle has tunneled beyond the classically forbidden region.

\[ \int_{5.22}^{ \infty} \psi (x, \alpha )^{2} dx \approx 1.879 \times 10^{-3} \nonumber \]

Calculate the probability that the particle is still in the nucleus.

\[ \int_{0}^{2} \psi (x, \alpha )^{2} dx \approx 0.764 \nonumber \]