8.56: A Brief Description of Aspect's Experiment
- Page ID
- 148207
The purpose of this tutorial is restricted to a brief computational summary of the EPR experiment reported by Aspect, Grangier and Roger, ʺExperimental Realization of Einstein‐Podolsky‐Rosen‐Bohm Gedanken Experiment: A New Violation of Bellʹs Inequalities,ʺ in Phys. Rev. Lett. 49, 91 (1982). See Chapter 6 of The Quantum Challenge by Greenstein and Zajonc, Chapter 4 of Jim Baggottʹs The Meaning of Quantum Theory, and Chapter 12 of Quantum Reality by Nick Herbert for complete analyses of this historically important experiment.
A two‐stage atomic cascade emits entangled photons (A and B) in opposite directions with the same circular polarization according to the observers in their path.
\[ | \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ |L \rangle_A |L \rangle_B + |R \rangle_A |R \rangle_B \right] \nonumber \]
The experiment involves the measurement of photon polarization states in the vertical/horizontal measurement basis, and allows that the polarization analyzers (PAs) can be oriented at different angles a and b. (The figure below is taken from Chapter 4 of Baggottʹs book.)

Naturally the bipartate photon wave function is identical in both the circular or linear polarization bases.
Left circular polarization:
\[ L = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} \nonumber \]
Right circular polarization:
\[ R = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} \nonumber \]
Vertical polarization:
\[ V = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
Horizontal polarization:
\[ H = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
\[ | \Psi \rangle = \frac{1}{2 \sqrt{2}} \left[ |L \rangle_A |L \rangle_B + |R \rangle_A |R \rangle_B \right] = \frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} 1 \\ i \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ i \end{pmatrix}_B + \begin{pmatrix} 1 \\ -i \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ -i \end{pmatrix}_B \right] = \frac{1}{ 2 \sqrt{2}} \left[ \begin{pmatrix} 1 \\ i \\ i \\ -1 \end{pmatrix} + \begin{pmatrix} 1 \\ -i \\ -i \\ -1 \end{pmatrix} \right] = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} \nonumber \]
\[ | \Psi \rangle = \frac{1}{2 \sqrt{2}} \left[ |V \rangle_A |V \rangle_B + |H \rangle_A |H \rangle_B \right] = \frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix}_B - \begin{pmatrix} 0 \\ 1 \end{pmatrix}_A \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix}_B \right] = \frac{1}{ 2 \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \right] = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} \nonumber \]
There are four measurement outcomes: both photons are vertically polarized, both are horizontally polarized, one is vertical and the other horizontal, and vice versa. The tensor representation of these measurement states are provided below.
\[ \begin{matrix} |VV \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} & |VH \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} & |HV \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} & |HH \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \end{matrix} \nonumber \]
We now write all states, Ψ and the measurement states, in Mathcad's vector format.
\[ \begin{matrix} \Psi = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} & \text{VV} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} & \text{VH} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} & \text{HV} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} & \text{HH} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \end{matrix} \nonumber \]
Next, the operator representing the rotation of PA1 by angle a clockwise and PA2 by angle b counter‐clockwise (so that the PAs turn in the same direction) is constructed using matrix tensor multiplication. Kronecker is Mathcadʹs command for tensor matrix multiplication.
\[ \text{RotOp(a, b)} = \text{kronecker} \left[ \begin{pmatrix} \cos a & \sin a \\ - \sin a & \cos a \end{pmatrix},~ \begin{pmatrix} \cos b & - \sin b \\ \sin b & \cos b \end{pmatrix} \right] \nonumber \]
The probability that the detectors will behave the same or differently is calculated as follows.
\[ \begin{matrix} P_{ \text{same}} (a,~ b) = \left( VV^T \text{RotOp(a, b)} \Psi \right)^2 + \left( HH^T \text{RotOp(a, b)} \Psi \right)^2 \\ P_{ \text{diff}} (a,~ b) = \left( VH^T \text{RotOp(a, b)} \Psi \right)^2 + \left( HV^T \text{RotOp(a, b)} \Psi \right)^2 \end{matrix} \nonumber \]
The expectation value as a function of the relative orientation of the polarization detectors is the difference between these two expressions. This is generally called the correlation function. In other words, the composite eigenvalues are: ++ = ‐‐ = +1 (same) and +‐ = ‐+ = ‐1 (diff).
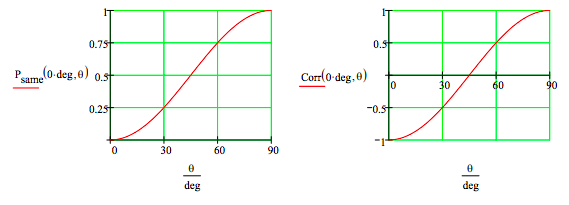
\[ \begin{matrix} \text{Corr(a, b)} = P_{same} \text{(a, b)} - P_{diff} \text{(a, b)} & \Theta = 0 \text{deg},~ 2 \text{deg}.. 90 \text{deg} \end{matrix} \nonumber \]
These graphical representations of the Aspect experiment are in agreement with those presented in Aspect's paper and also in The Quantum Challenge, The Meaning of Quantum Theory, and Quantum Reality.
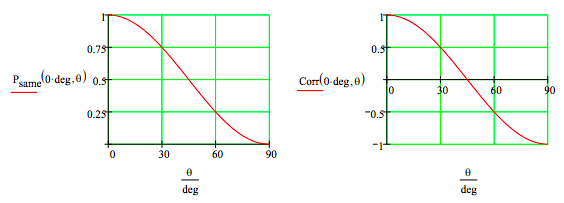
These calculations are now repeated for the three other Bell states.
\[ \begin{matrix} \Psi = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 0 & 0 & 1 \end{pmatrix}^T \\ P_{same} \text{(a, b)} = \left( VV^T \text{RotOp(a, b)} \Psi \right)^2 + \left( HH^T \text{RotOp(a, b)} \Psi \right)^2 \\ P_{diff} \text{(a, b)} = \left( VH^T \text{RotOp(a, b)} \Psi \right)^2 + \left( HV^T \text{RotOp(a, b)} \Psi \right)^2 \\ \text{Corr(a, b)} = P_{same} \text{(a, b)} - P_{diff} \text{(a, b)} \end{matrix} \nonumber \]
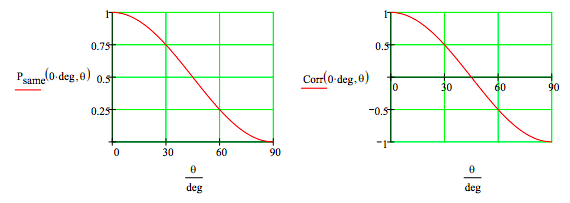
\[ \begin{matrix} \Psi = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 & 1 & 1 & 0 \end{pmatrix}^T \\ P_{same} \text{(a, b)} = \left( VV^T \text{RotOp(a, b)} \Psi \right)^2 + \left( HH^T \text{RotOp(a, b)} \Psi \right)^2 \\ P_{diff} \text{(a, b)} = \left( VH^T \text{RotOp(a, b)} \Psi \right)^2 + \left( HV^T \text{RotOp(a, b)} \Psi \right)^2 \\ \text{Corr(a, b)} = P_{same} \text{(a, b)} - P_{diff} \text{(a, b)} \end{matrix} \nonumber \]
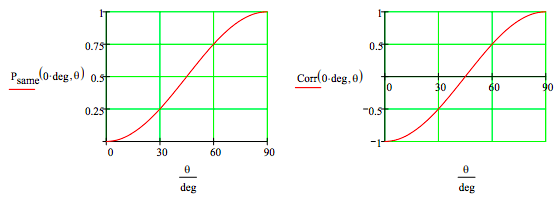
\[ \begin{matrix} \Psi = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 & 1 & -1 & 0 \end{pmatrix}^T \\ P_{same} \text{(a, b)} = \left( VV^T \text{RotOp(a, b)} \Psi \right)^2 + \left( HH^T \text{RotOp(a, b)} \Psi \right)^2 \\ P_{diff} \text{(a, b)} = \left( VH^T \text{RotOp(a, b)} \Psi \right)^2 + \left( HV^T \text{RotOp(a, b)} \Psi \right)^2 \\ \text{Corr(a, b)} = P_{same} \text{(a, b)} - P_{diff} \text{(a, b)} \end{matrix} \nonumber \]