2.54: Quantum Calculations on the Hydrogen Atom in Coordinate, Momentum and Phase Space
- Page ID
- 156421
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Coordinate Space Operators
| Position operator: \(x \cdot \Box\) | Momentum operator: \(\mathrm{p}=\frac{1}{\mathrm{i}} \cdot \frac{\mathrm{d}}{\mathrm{dx}} \Box\) | Integral: \(\int_{0}^{\infty} \Box d x\) |
| Kinetic energy operator: \(\mathrm{KE}=-\frac{1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{x}^{2}} \Box\) | Potential energy operator: \(\mathrm{PE}=\frac{-1}{\mathrm{x}} \Box\) |
The energy operator for the one‐dimensional hydrogen atom in atomic units is:
\[
\frac{-1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{x}^{2}} \Box-\frac{1}{\mathrm{x}} \cdot \Box
\nonumber \]
The ground state wave function in coordinate space is:
\[
\Psi(x) :=2 \cdot x \cdot \exp (-x)
\nonumber \]
Display the coordinate‐space distribution function:
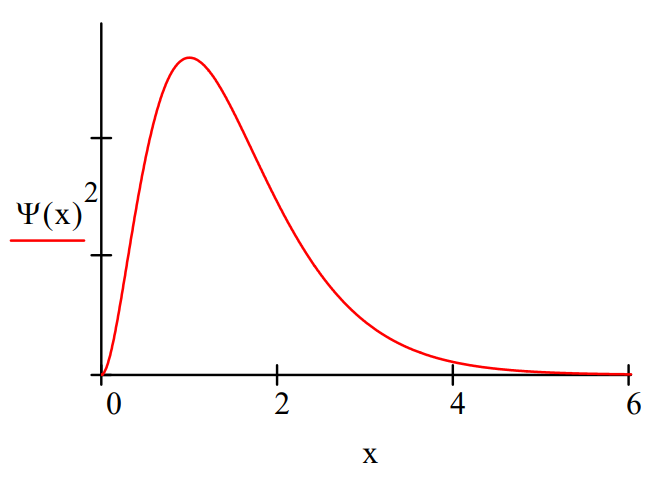
The ground state energy is ‐0.5 Eh.
\[
\frac{-1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{x}^{2}} \Psi(\mathrm{x})-\frac{1}{\mathrm{x}} \cdot \Psi(\mathrm{x})=\mathrm{E} \cdot \Psi(\mathrm{x}) \text { solve, } \mathrm{E} \rightarrow \frac{-1}{2}
\nonumber \]
The coordinate wave function is normalized:
\[
\int_{0}^{\infty} \Psi(x)^{2} d x=1
\nonumber \]
The expectation value for position:
\[
\int_{0}^{\infty} x \cdot \Psi(x)^{2} d x=1.5
\nonumber \]
The expectation value for momentum:
\[
\int_{0}^{\infty} \Psi(x) \cdot \frac{1}{i} \cdot \frac{d}{d x} \Psi(x) d x=0
\nonumber \]
The expectation value for kinetic energy:
\[
\int_{0}^{\infty} \Psi(x) \cdot \frac{-1}{2} \cdot \frac{d^{2}}{d x^{2}} \Psi(x) d x=0.5
\nonumber \]
The expectation value for potential energy:
\[
\int_{0}^{\infty} \frac{-1}{x} \cdot \Psi(x)^{2} d x=-1
\nonumber \]
The momentum wave function is generated by the following Fourier transform of the coordinate space wave function.
\[
\Phi(p) :=\frac{1}{\sqrt{2 \cdot \pi}} \int_{0}^{\infty} \exp (-i \cdot p \cdot x) \cdot \Psi(x) d x \rightarrow \frac{2^{\frac{1}{2}}}{\pi^{\frac{1}{2}} \cdot(i \cdot p+1)^{2}}
\nonumber \]
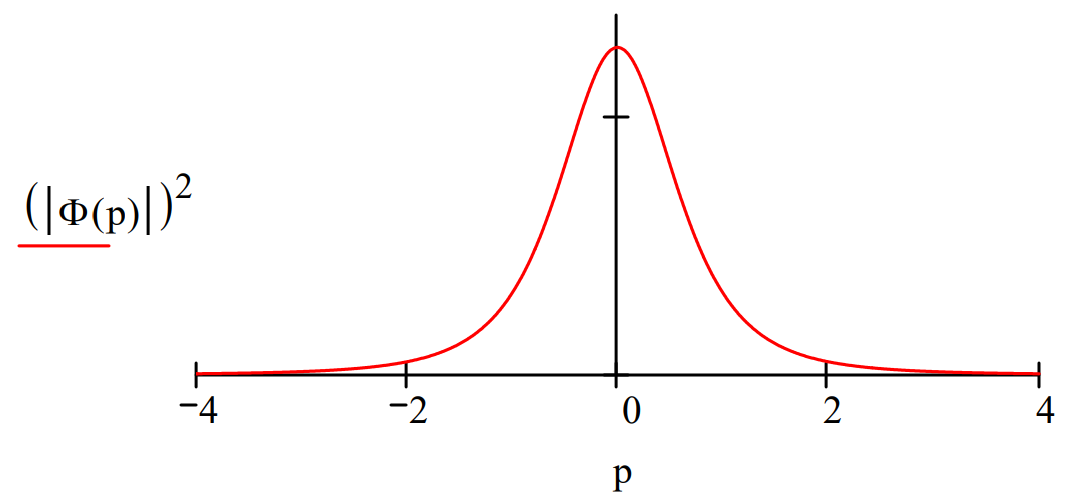
Momentum Space Operators
| Momentum space integral: \(\int_{-\infty}^{\infty} \Box \mathrm{dp}\) | Momentum operator: \(p \cdot \Box\) |
| Kinetic energy operator: \(\frac{\mathrm{p}^{2}}{2}\) | Position operator: \(i \cdot \frac{\mathrm{d}}{\mathrm{dp}} \Box\) |
The same calculations made with the momentum space wave function:
The momentum wave function is normalized:
\[
\int_{-\infty}^{\infty}(|\Phi(p)|)^{2} d p=1
\nonumber \]
The expectation value for position:
\[
\int_{-\infty}^{\infty} \overline{\Phi(p)} \cdot i \cdot \frac{d}{d p} \Phi(p) d p=1.5
\nonumber \]
The expectation value for momentum:
\[
\int_{-\infty}^{\infty} p \cdot(|\Phi(p)|)^{2} d p=0
\nonumber \]
The expectation value for kinetic energy:
\[
\int_{-\infty}^{\infty} \frac{\mathrm{p}^{2}}{2} \cdot(|\Phi(\mathrm{p})|)^{2} \mathrm{dp}=0.5
\nonumber \]
The Wigner function for the hydrogen atom ground state is generated using the momentum wave function.
\[
\mathrm{W}(\mathrm{x}, \mathrm{p}) :=\frac{1}{2 \cdot \pi} \cdot \int_{-\infty}^{\infty} \overline{\Phi\left(\mathrm{p}+\frac{\mathrm{s}}{2}\right)} \cdot \exp (-\mathrm{i} \cdot \mathrm{s} \cdot \mathrm{x}) \cdot \Phi\left(\mathrm{p}-\frac{\mathrm{s}}{2}\right) \mathrm{ds}
\nonumber \]
The Wigner distribution is displayed graphically.
\[
\mathrm{N} :=60 \qquad \mathrm{i} :=0 . . \mathrm{N} \qquad \mathrm{x}_{\mathrm{i}} :=\frac{6 \cdot \mathrm{i}}{\mathrm{N}} \\ \mathrm{j} :=0 . . \mathrm{N} \qquad \mathrm{p}_{\mathrm{j}} :=-5+\frac{10 \cdot \mathrm{j}}{\mathrm{N}} \qquad \text{Wigner}_{\text {i ,j }} :=\mathrm{W}\left(\mathrm{x}_{i}, \mathrm{p}_{\mathrm{j}}\right)
\nonumber \]
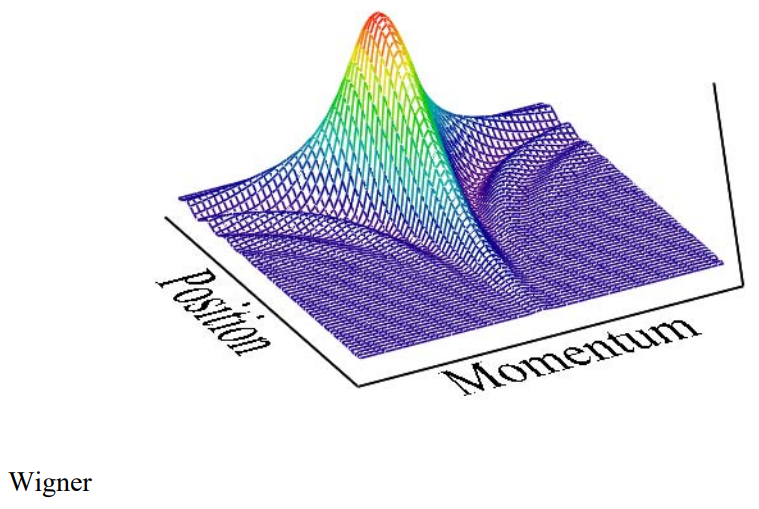
One of the interesting features of doing quantum mechanics with the Wigner distribution is that the position and momentum operators retain their classical forms; they are both multiplicative operators. By comparison in the coordinate representation position is multiplicative and momentum is differential. In the momentum representation itʹs the reverse. This is illustrated below with the following calculations.
| Phase space integral: \(\int_{-\infty}^{\infty} \int_{0}^{\infty} \Box d x d p\) | Position operator: \(x \cdot \Box\) | Momentum operator: \(p \cdot \Box\) |
| Kinetic energy operator: \(\mathrm{KE}=\frac{\mathrm{p}^{2}}{2} \cdot \Box\) | Potential energy operator: \(\mathrm{PE}=\frac{-1}{\mathrm{x}} \cdot \Box\) |
Phase space calculations using the Wigner distribution:
The Wigner distribution is normalized:
\[
\int_{-\infty}^{\infty} \int_{0}^{\infty} W(x, p) d x d p=1
\nonumber \]
The expectation value for position:
\[
\int_{-\infty}^{\infty} \int_{0}^{\infty} x \cdot W(x, p) d x d p=1.5
\nonumber \]
The expectation value for momentum:
\[
\int_{-\infty}^{\infty} \int_{0}^{\infty} p \cdot W(x, p) d x d p=0
\nonumber \]
The expectation value for kinetic energy:
\[
\int_{-\infty}^{\infty} \int_{0}^{\infty} \frac{p^{2}}{2} \cdot W(x, p) dx dp=0.5
\nonumber \]
The expectation value for potential energy:
\[
\int_{-\infty}^{\infty} \int_{0}^{\infty} \frac{-1}{x} \cdot W(x, p) d x d p=-1
\nonumber \]