2.49: Momentum Wavefunctions and Distributions for the Hydrogen Atom
- Page ID
- 158384
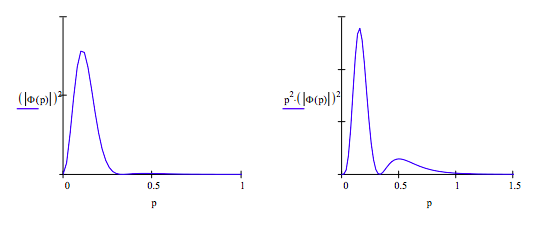
The Fourier transform for the 1s orbital
\[ \Phi (p) = \frac{1}{ \sqrt{8 \pi^4}} \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \text{exp(-r) exp} \left( - \text{i p r} \cos \left( \theta \right) \right) r^2 \sin \left( \theta \right) d \phi d \theta dr \rightarrow \frac{2^{ \frac{1}{2}}}{ \pi \left[ (-1) + \text{i p} \right]^2 (1 + \text{i p}^2} \nonumber \]
p = 0, .02 .. 5
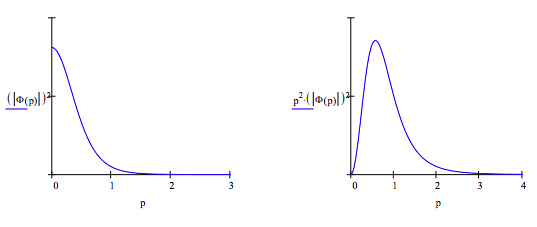
The Fourier transform for the 2s orbital
\[ \Phi (p) = \frac{1}{16 \pi^2} \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} (2 - r) \text{exp} \left( - \frac{r}{2} \right) \text{exp} \left( \text{-i p r} \cos \left( \theta \right) \right) r^2 \sin ( \theta ) d \phi d \theta dr \nonumber \]
\[ \begin{matrix} \text{yields} & \Phi (p) = \frac{-16}{ \pi} \frac{(-1) + 4p^2}{[(-1) + 2 \text{i p}]^3 (1 + 2 \text{i p})^3} & p = 0, .02 .. 2 \end{matrix} \nonumber \]
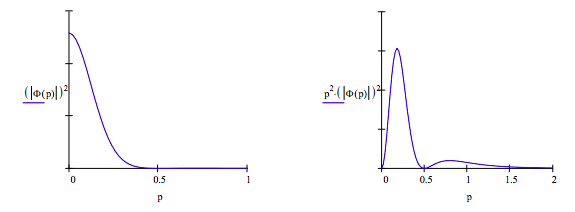
The Fourier transform for the 2pz orbital
\[ \Phi (p) = \frac{1}{16 \pi^2} \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \text{r exp} \left( - \frac{r}{2} \right) \text{exp} \left( \text{-i p r} \cos \left( \theta \right) \right) r^2 \sin ( \theta ) d \phi d \theta dr \nonumber \]
\[ \begin{matrix} \text{yields} & \Phi (p) = 64 \frac{i}{ \pi} \frac{p}{[(-1) + 2 \text{i p}^3 (1 + 2 \text{i p}^3} \end{matrix} \nonumber \]
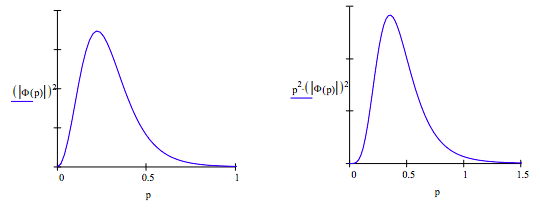
The Fourier transform for the 3s orbital
\[ \Phi (p) = \frac{1}{162 \sqrt{2} \pi^2} \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \left( 27 - 18r + 2r^2 \right) \text{exp} \left( - \frac{r}{3} \right) \text{exp} \left( \text{-i p r} \cos \left( \theta \right) \right) r^2 \sin ( \theta ) d \phi d \theta dr \nonumber \]
\[ \begin{matrix} \text{yields} & \Phi (p) = 18 \frac{6^{ \frac{1}{2}}}{ \pi} \frac{(-30)p^2 + 1 + 81p^4}{[(-1) + 3 \text{i p}]^4 (1 + 3 \text{i p})^4} \end{matrix} \nonumber \]
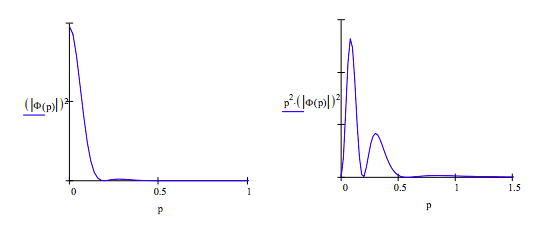
The Fourier transform for the 3pz orbital
\[ \Phi (p) = \frac{1}{162 \pi^2} \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \left( 6r -r^2 \right) \text{ exp} \left( - \frac{r}{3} \right) \text{exp} \left( \text{-i p r} \cos \left( \theta \right) \right) \cos \left( \theta \right) r^2 \sin ( \theta ) d \phi d \theta dr \nonumber \]
\[ \begin{matrix} \text{yields} & \Phi (p) = (-432) \frac{i}{ \pi} p \frac{9p^2 - 1}{[(-1) + 3 \text{i p}]^4 (1 + 3 \text{i p})^4} \end{matrix} \nonumber \]