2.48: How Many Bibles Can Fit on the Head of a Pin
- Page ID
- 158383
On December 29, 1959 Richard Feynman gave an address (Thereʹs Plenty of Room at the Bottom) in which he calculated how many Encyclopedia Britannicas could fit on the head of a pin. Legend identifies this event as the beginning of the field of theoretical nanotechnology.
To illustrate to general chemistry students how small nanoscopic entities, such as atoms, are I calculate with the following simple model how many bibles can fit on the head of a pin.
The model assumes that the pinhead surface is made up of Fe atoms packed in a simple squaric array. It further assumes that letters would be made by placing adatoms in the pockets created by the surface Fe atoms using a scanning tunneling microscope, and that 100 pinhead surface Fe atoms would be required to form a letter.
The first step is to calculate the number of Fe atoms on the pinhead.
\[ \begin{matrix} \text{Radium of pinhead:} & R_{PH} = \frac{1}{32} in & R_{PH} = 7.94 \times 10^8 pm \\ \text{Area of pinhead:} & \text{Area}_{PH} = \pi R_{PH}^2 & \text{Area}_{PH} = 1.98 \times 10^{18} \text{pm}^3 \\ \text{Radius of Fe:} & \text{R}_{Fe} = 126 \text{pm} & \text{R}_{Fe} = 1.26 \times 10^{-10} \text{pm} \\ \text{Area of Fe atom:} & \text{Area}_{Fe} = \pi \text{R}_{Fe}^2 & \text{Area}_{Fe} = 4.99 \times 10^4 \text{pm}^2 \end{matrix} \nonumber \]
Effective area of Fe atom:
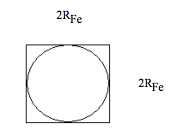
\[ \begin{matrix} \text{EffectiveArea}_{Fe} = 4 \text{R}_{Fe}^2 \\ \text{EffectiveArea}_{Fe} = 6.35 \times 10^4 \text{pm}^2 \end{matrix} \nonumber \]
Fe atoms per pinhead:
\[ \begin{matrix} \text{FeAtomsPerPinHead} = \frac{ \text{Area}_{PH}}{ \text{EffectiveArea}_{Fe}} & \text{FeAtomsPerPinHead} = 3.12 \times 10^{13} \end{matrix} \nonumber \]
A typical family Bible consists of 1,000 pages with an average of 5,000 characters and spaces per page. If it takes 100 Fe atoms to define a character, how many Bibles can fit on the head of a pin?
\[ \begin{matrix} \text{PagesPerBible} = 1000 & \text{CharactersPerPage} = 5000 & \text{FeAtomsPerCharacter} = 100 \end{matrix} \nonumber \]
Fe atoms required per bible:
\[ \begin{matrix} \text{FeAtomsPerCharacter CharactersPerPage PagesPerBible} = 5 \times 10^8 \\ \text{BiblesPerPinHead} = \frac{ \text{FeAtomsPerPinHead}}{ \text{FeAtomsPerCharacter CharactersPerPage PagesPerBible}} \\ \text{BiblesPerPinHead} = 6.2 \times 10^4 \end{matrix} \nonumber \]
Define picometer: \( \text{pm} = 10^{-12} \text{m}\)

