2.22: The Hydrogen Atom with Finite Sized Nucleus
- Page ID
- 155900
This exercise explores the impact of nuclear size on the ground state energy of the hydrogen atom's electron. The traditional approach assumes that the proton is a dimensionless point charge, which is a very good approximation for the hydrogen atom. However, for heavy atoms with many protons and neutrons, the finite size of the nucleus has to be taken into consideration when the goal is exact results. If the proton has uniform charge density and is given a finite radius, the potential energy of the electron is as given below.
Nuclear radius: Rn = 0.1
Potential energy:
\[ V(r) = \text{if} \left[ r \leq \text{Rn},~ \frac{-1}{ \text{Rn}} \left( 1.5 - \frac{r^2}{2 Rn^2} \right),~ \frac{-1}{r} \right] \nonumber \]
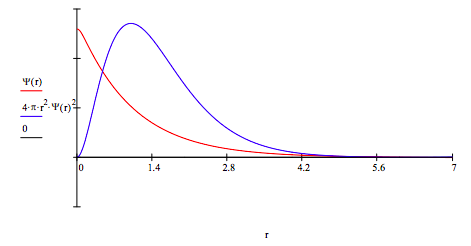
Numerical integration of Schrödinger's equation (see below) yields the following results.
\[ \begin{pmatrix} \frac{ \text{Nuclear Radius}}{a_o} 0 & 0.1 & 0.2 & 0.5 & 1.0 & 2.0 \\ \frac{ \text{Energy}}{E_h} & -0.500 & -0.496 & -0.488 & -0.450 & -0.385 & -0.293 \end{pmatrix} \nonumber \]
A recommended exercise is to repeat these calculations for the 2s and 3s electronic states, and interpret the results.
Numerical integration of Schrödinger's equation:
\[ \begin{matrix} \text{Given} & \frac{-1}{2 \mu} \frac{d^2}{dr^2} \Psi (r) & - \frac{1}{r \mu} \frac{d}{dr} \Psi (r) + \left[ \frac{L(L+1)}{2 \mu r^2} + V(r) \right] \Psi (r) = E \Psi (r) & \Psi (.0001) = .1 & \Psi (.0001) = 0 \end{matrix} \nonumber \]
\[ \Psi = \text{Odesolve} \left( r,~ r_{max} \right) \nonumber \]
Normalize the wave function:
\[ \Psi (r) = \left( \int_0^{r_{max}} \Psi (r)^2 4 \pi r^2 dr \right)^{-.5} \Psi (r) \nonumber \]
\[ \begin{matrix} \text{Reduced mass:} & \mu = 1 & \text{Angular momentum:} & L = 0 & \text{Integration limit:} & r_{max} = 7 \\ \text{Energy guess:} & E = -0.496 & r = 0,~.01 .. r_{max} \end{matrix} \nonumber \]