1.93: Wave-particle Duality and the Uncertainty Principle
- Page ID
- 158512
Nick Herbert, author of Quantum Reality, has proposed the name quon for "any entity that exhibits both wave and particle attributes in the peculiar quantum mechanical manner." Obvious examples of quons for chemists are the electron, proton, neutron and photon. The wave-particle duality of quons is captured succinctly by the deBroglie relation, which unites the wave property \(\lambda\) with the particle property mv in a reciprocal relationship mediated by the ubiqutous Planck's constant.
\[
\lambda=\frac{\mathrm{h}}{\mathrm{mv}}=\frac{\mathrm{h}}{\mathrm{p}}
\nonumber \]
The most general momentum wave function for a quon in one-dimension is Euler's equation when it incorporates the deBroglie equation.
\[
\langle x | p\rangle=\exp \left(i 2 \pi \frac{x}{\lambda}\right) \frac{\lambda=h / p}{\hbar= h/ 2 \pi} \exp \left(\frac{i p x}{\hbar}\right)=\cos \left(\frac{p x}{\hbar}\right)+i \sin \left(\frac{p x}{\hbar}\right) \\ \Psi(p, x) :=\exp (i p \cdot x)
\nonumber \]
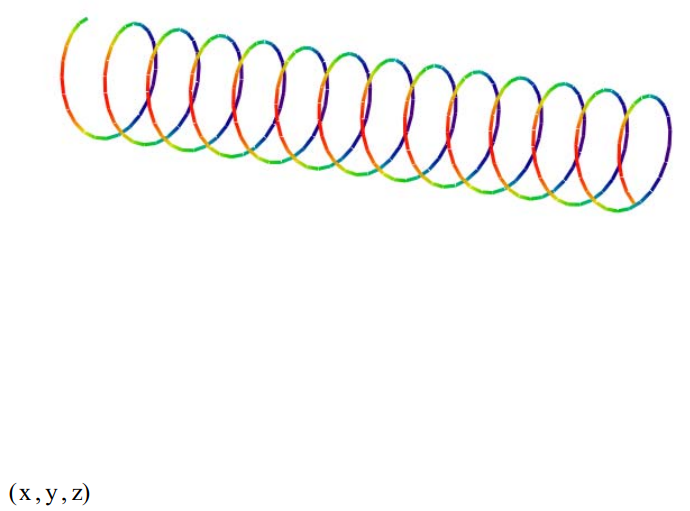
The momentum wave function for a quon with a well-defined momentum (p = 7, for example) is shown below in atomic units (h = 2\(\pi\)). It clearly illustrates the uncertainty principle because the wave function is completely spatially delocalized.
Momentum:
\[
\mathrm{p} :=7 \qquad \mathrm{j} :=0 \ldots 300
\nonumber \]
Axis of propagation:
\[
\mathrm{x}_{\mathrm{j}} :=\mathrm{j} \cdot 0.04
\nonumber \]
Real axis:
\[
\mathrm{y}_{\mathrm{j}} :=\operatorname{Re}\left(\Psi\left(\mathrm{p}, \mathrm{x}_{\mathrm{j}}\right)\right)
\nonumber \]
Imaginary axis:
\[
z_{\mathrm{j}} :=\operatorname{Im}\left(\Psi\left(\mathrm{p}, \mathrm{x}_{\mathrm{j}}\right)\right)
\nonumber \]
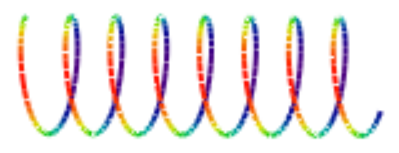
As might be expected on the basis of the uncertainty principle, the particle-like character of a quon is revealed only when there is uncertainty in momentum. This can be demonstrated by plotting Euler's equation for a superposition of momentum states as shown below. This superposition (integrating, or summing over a range of momentum values) clearly reveals the incipient particle-like characteristics of a quon.
Axis of propagation:
\[
x_{j} :=j \cdot 0.054-7
\nonumber \]
Real axis:
\[
\mathrm{y}_{\mathrm{j}} :=\int_{6}^{8} \operatorname{Re}\left(\Psi\left(\mathrm{p}, \mathrm{x}_{\mathrm{j}}\right)\right) \mathrm{d} \mathrm{p}
\nonumber \]
Imaginary axis:
\[
z_{j} :=\int_{6}^{8} \operatorname{Im}\left(\Psi\left(p, x_{j}\right)\right) d p
\nonumber \]

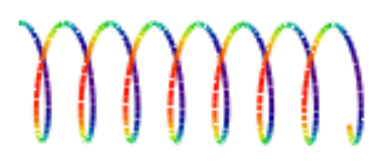
The form of Euler's equation we have been using, \(<\mathrm{x} | \mathrm{p}>\), is the momentum eigenfunction in coordinate space. Its complex conjugate, \(<\mathrm{p} | \mathrm{x}>\), is the position eigenfunction in momentum space. In other words, a quon with a well-defined position is delocalized in momentum space, just as a quon with a well-defined momentum is delocalized in coordinate space.
\[
\langle x | p\rangle=\exp \left(\frac{i p x}{\hbar}\right)
\nonumber \]
\[
\langle p | x\rangle=\exp \left(-\frac{i p x}{\hbar}\right)
\nonumber \]
These equations are simple Fourier transforms; they allow us to translate knowledge in one language (position or momentum) into the other language. They are a kind of mathematical dictionary. Richard Feynman claimed that Euler's equation is the most remarkable equation in mathematics and called it "our jewel." Because it is the kernel in Fourier transforms, it is ubiquitous in quantum mechanics.

