1.78: Coherent Superpositions for the Harmonic Oscillator
- Page ID
- 156479
The quantum mechanical harmonic oscillator eigenstates are stationary states and therefore cannot be used individually to represent classical oscillatory motion. (Atomic units are used in this tutorial.)
\[
\Psi(v, x, t) :=\frac{1}{\sqrt{2^{v} \cdot v ! \cdot \sqrt{\pi}}} \cdot \operatorname{Her}(v, x) \cdot \exp \left(\frac{-x^{2}}{2}\right) \cdot \exp \left[-i \cdot\left(v+\frac{1}{2}\right) \cdot t\right]
\nonumber \]
For example, suppose we choose to represent the ground vibrational state of a homonuclear diatomic mole as a simple harmonic oscillator with vibrational quantum number v = 0. We see that probability distributio \(|\Psi(0, x, t)|^{2}\), is independent of time. There is no oscillatory motion; the molecule is in a stationary state whic weighted superposition of all possible internuclear separations.
However, simple superpositions of the vibrational eigenstates do show oscillatory behavior. This is due to exponential term involving the vibrational energy, exp[-iE(v)t]. This term oscillates with a dependence on vibrational quantum number. Thus, the different eigenstates oscillate with different frequencies giving rise constructive and destructive intereference. The figures below show the time dependence of the v = 0/v =1 the v = 0/v = 2 superpositions. Both show oscillatory behavior, but the first is asymmetric and the second i symmetric. This has significance for harmonic oscillator selection rules, as will be discussed below.
\[
\operatorname{Sup}(\mathrm{x}, \mathrm{t}) :=\frac{\Psi(0, \mathrm{x}, \mathrm{t})+\Psi(1, \mathrm{x}, \mathrm{t})}{\sqrt{2}}
\nonumber \]
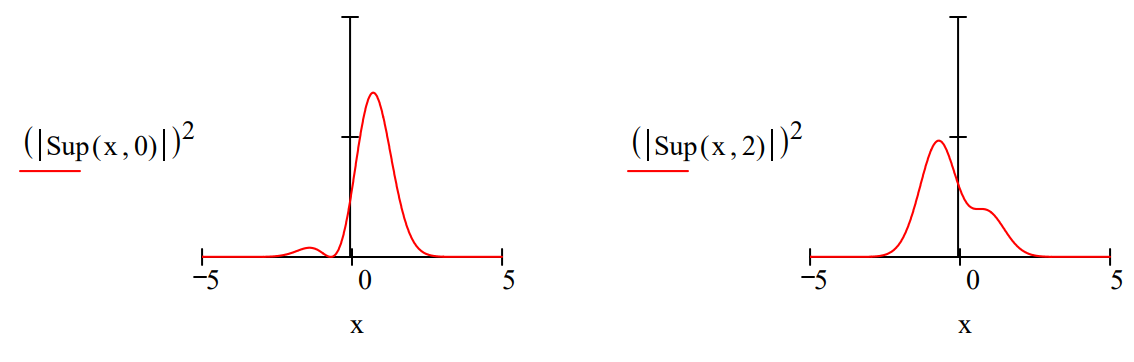
The asymmetry of this time-dependent probability distribution gives it electric oscillating dipole character mechanism for coupling with the oscillating dipole of the electromagnetic field. Thus we could argue this i basis for the fact that the v = 0 to v = 1 vibrational transition is allowed.
\[
\operatorname{Sup}(\mathrm{x}, \mathrm{t}) :=\frac{\Psi(0, \mathrm{x}, \mathrm{t})+\Psi(2, \mathrm{x}, \mathrm{t})}{\sqrt{2}}
\nonumber \]
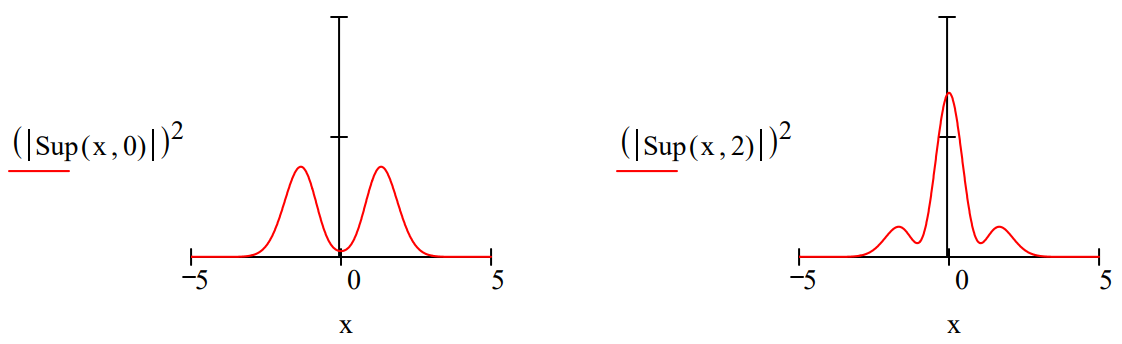
By comparison the symmetry of this time-dependent probability distribution does not have oscillatory dipo character, so there is no coupling with the external electromagnetic field. Therefore, the v = 0 to v = 2 vibrational transition is formally forbidden. Further detail on this interpretation of the "quantum jump" can found in the Spectroscopy section of Quantum Potpourri.
By comparison, coherent states (also called Glauber states) of the harmonic oscillator are more elaborate superpositions that maintain the well-defined shape of the ground state distribution while exhibiting the ki classical oscillatory motion that is absent in the previous examples. The time-dependence and "classical" oscillatory behavior of a coherent superposition of 25 vibrational eigenstates is illustrated below. See any contemporary text on quantum optics for further information on coherent states of the harmonic oscillator.
\[
\mathrm{n} :=25 \qquad \mathrm{x} :=-8,-7.98\ldots8 \qquad \alpha :=3.5
\nonumber \]
\[
\Psi(x, t) :=\frac{1}{\sqrt{n}} \cdot \exp \left(\frac{-x^{2}}{2}\right) \cdot \exp \left(\frac{-\alpha^{2}}{2}\right)\cdot\sum_{v=0}^{n}\left[\operatorname{Her}(v, x) \cdot \exp \left[-i \cdot\left(v+\frac{1}{2}\right) \cdot t\right] \cdot \frac{\alpha^{v}}{v ! \cdot \sqrt{2^{v} \cdot \sqrt{2}}}\right]
\nonumber \]
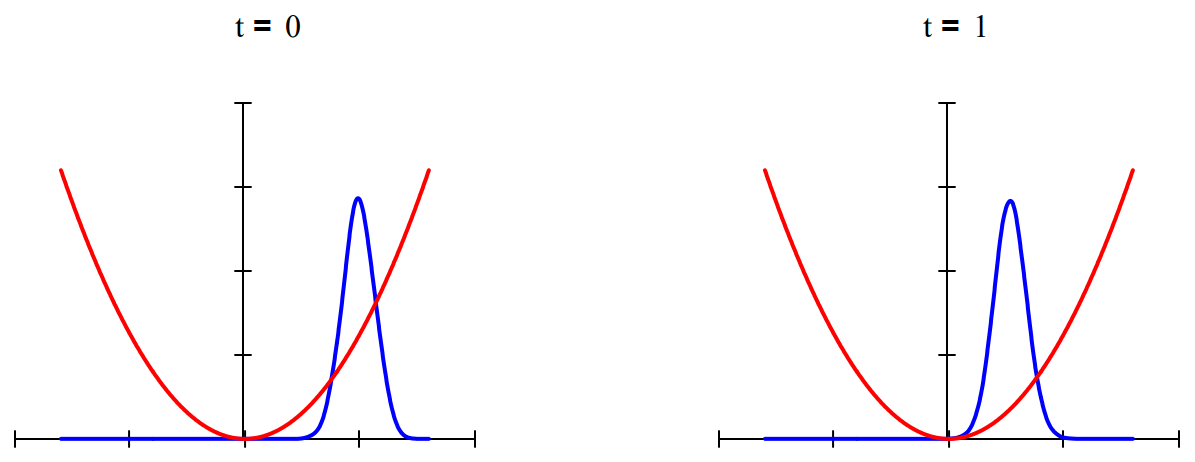
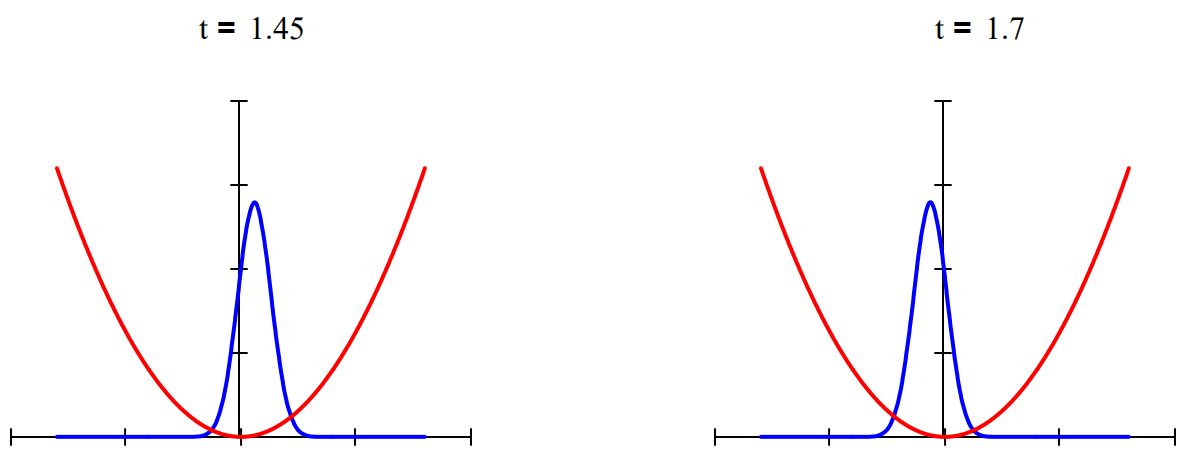
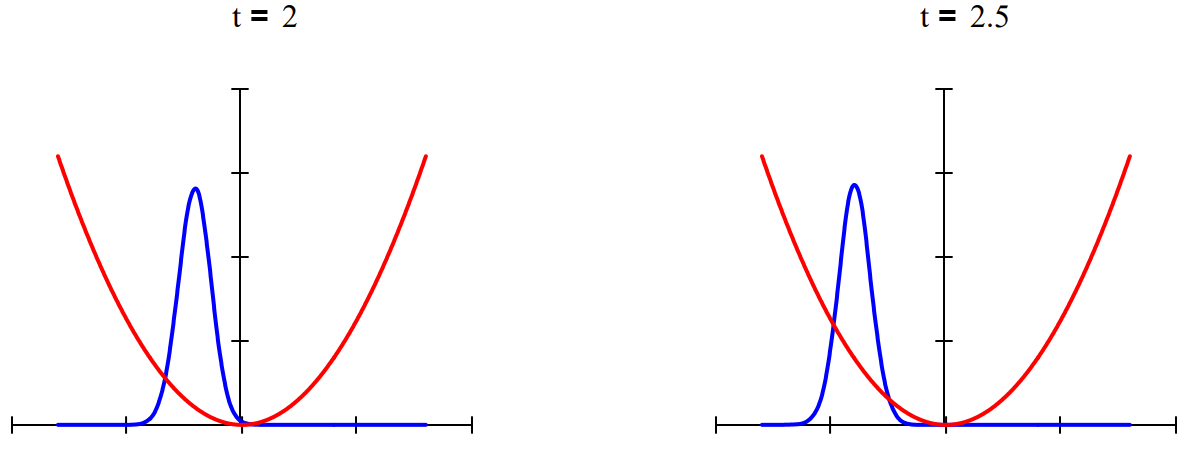
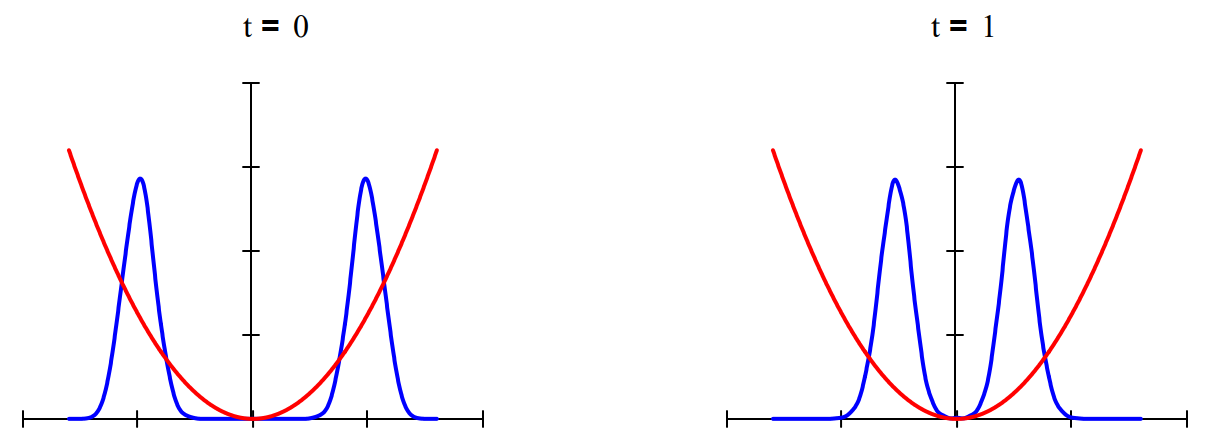
Time-dependent superpositions of coherent states have been used to model Schrödinger cat states. Below w show the interaction of two coherent states moving in opposite directions from opposite sides of a harmoni potential well. The interference observed when they meet in the middle has been observed experimentally Bose-Einstein condensates.
\[
\alpha :=3.5 \qquad \qquad \beta :=-3.5
\nonumber \]
\[
\Psi(x, t) :=\frac{1}{\sqrt{n}} \cdot \exp \left(\frac{-x^{2}}{2}\right) \cdot \exp \left(\frac{-\alpha^{2}}{2}\right) \cdot \sum_{v=0}^{n}\left[\operatorname{Her}(v, x) \cdot \exp \left[-i \cdot\left(v+\frac{1}{2}\right) \cdot t\right] \cdot \frac{\alpha^{v}}{v ! \cdot \sqrt{2^{v} \cdot \sqrt{2}}}\right] \\ +\frac{1}{\sqrt{n}} \cdot \exp \left(\frac{-\mathrm{x}^{2}}{2}\right) \exp \left(\frac{-\beta^{2}}{2}\right) \cdot \sum_{\mathrm{v}=0}^{\mathrm{n}}\left[\operatorname{Her}(\mathrm{v}, \mathrm{x}) \cdot \exp \left[-\mathrm{i} \cdot\left(\mathrm{v}+\frac{1}{2}\right) \cdot \mathrm{t}\right] \cdot \frac{\beta^{\mathrm{v}}}{\mathrm{v} ! \cdot \sqrt{2^{\mathrm{v}} \cdot \sqrt{2}}}\right]
\nonumber \]
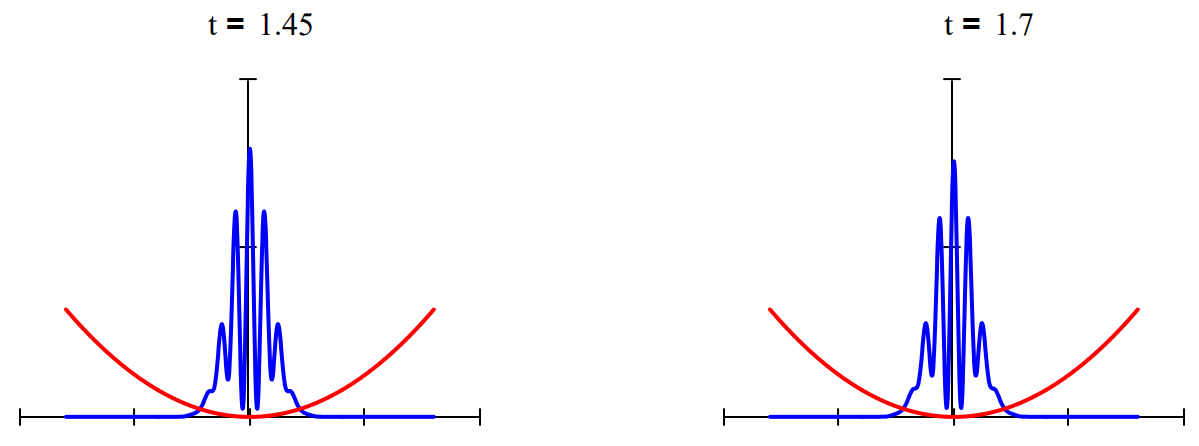
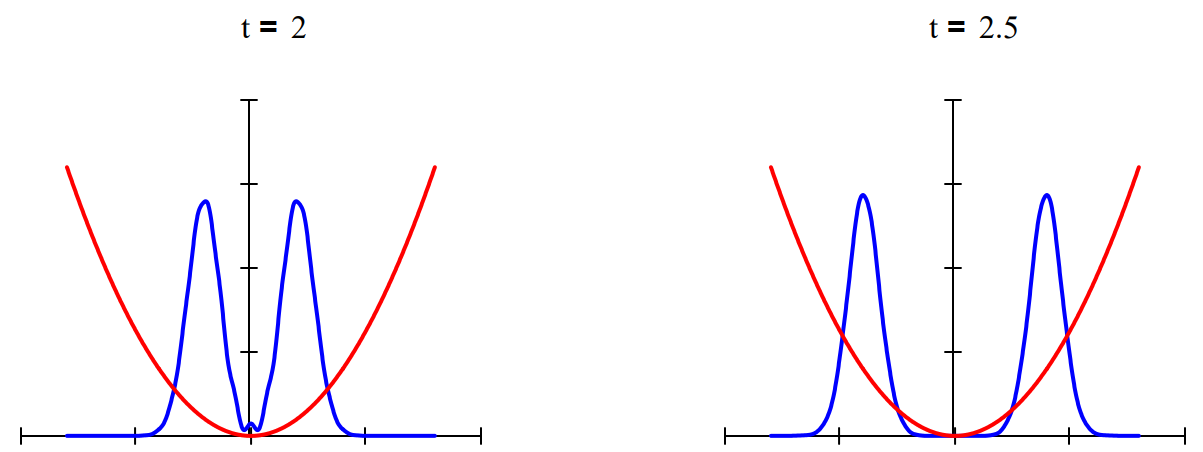
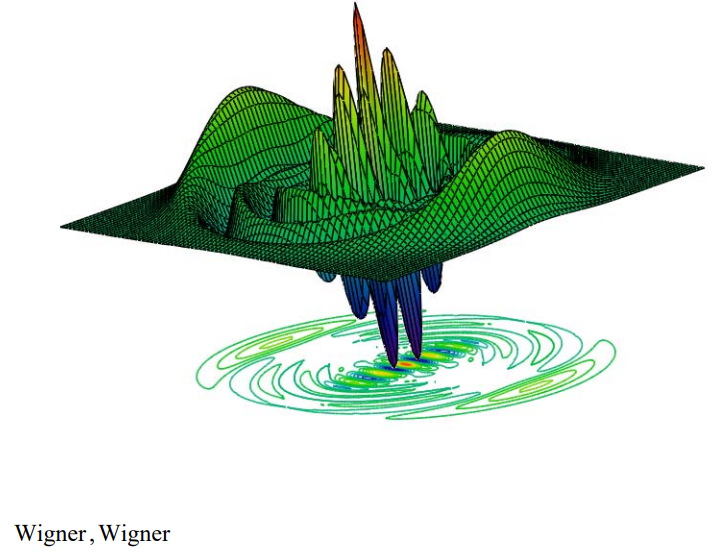
We finish with a calculation of the Wigner phase-space distribution for a Schrödinger cat state at t = 0. In t interest of computational expediency a superposition of only 10 harmonic eigenstates is calculated. The Wigner function is itself a superposition of all phase-space trajectories and is called a quasi probability distribution because it can take on negative values as is shown in the figure below. The interference fringe the center are closely related to those that appear in the figures above.
\[
\Psi(\mathrm{x}) :=\frac{1}{\sqrt{\mathrm{n}}} \cdot \exp \left(\frac{-\mathrm{x}^{2}}{2}\right) \cdot \exp \left(\frac{-\alpha^{2}}{2}\right) \cdot \sum_{\mathrm{v}=0}^{10}\left(\operatorname{Her}(\mathrm{v}, \mathrm{x}) \cdot \frac{\alpha^{\mathrm{v}}}{\mathrm{v} ! \cdot \sqrt{2^{\mathrm{v}} \cdot \sqrt{2}}}\right) \\ +\left[\frac{1}{\sqrt{\mathrm{n}}} \cdot \exp \left(\frac{-\mathrm{x}^{2}}{2}\right) \cdot \exp \left(\frac{-\beta^{2}}{2}\right) \cdot \sum_{\mathrm{v}=0}^{10}\left(\operatorname{Her}(\mathrm{v}, \mathrm{x}) \cdot \frac{\beta^{\mathrm{v}}}{\mathrm{v} ! \cdot \sqrt{2^{\mathrm{v}} \cdot \sqrt{2}}}\right)\right]
\nonumber \]
Wigner distribution:
\[
\mathrm{W}(\mathrm{x}, \mathrm{p}) :=\frac{1}{\pi^{\frac{3}{2}}} \cdot \int_{-\infty}^{\infty} \Psi\left(\mathrm{x}+\frac{\mathrm{s}}{2}\right) \cdot \exp (\mathrm{i} \cdot \mathrm{s} \cdot \mathrm{p}) \cdot \Psi\left(\mathrm{x}-\frac{\mathrm{s}}{2}\right) \mathrm{ds}
\nonumber \]
\[
\mathrm{N} :=80 \qquad \mathrm{i} :=0 \ldots\mathrm{N} \quad \mathrm{x}_{\mathrm{i}} :=-5+\frac{10 \cdot \mathrm{i}}{\mathrm{N}} \\ \mathrm{j} :=0 \ldots \mathrm{N} \qquad \mathrm{p}_{\mathrm{j}} :=-5+\frac{10 \cdot \mathrm{j}}{\mathrm{N}} \qquad \text { Wigner}_{\mathrm{i},\mathrm{j}} :=\mathrm{W}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{p}_{\mathrm{j}}\right)
\nonumber \]